Предмет: Алгебра,
автор: danilrostnd
помогите закончить решение уравнения (задание во вложении)
Приложения:
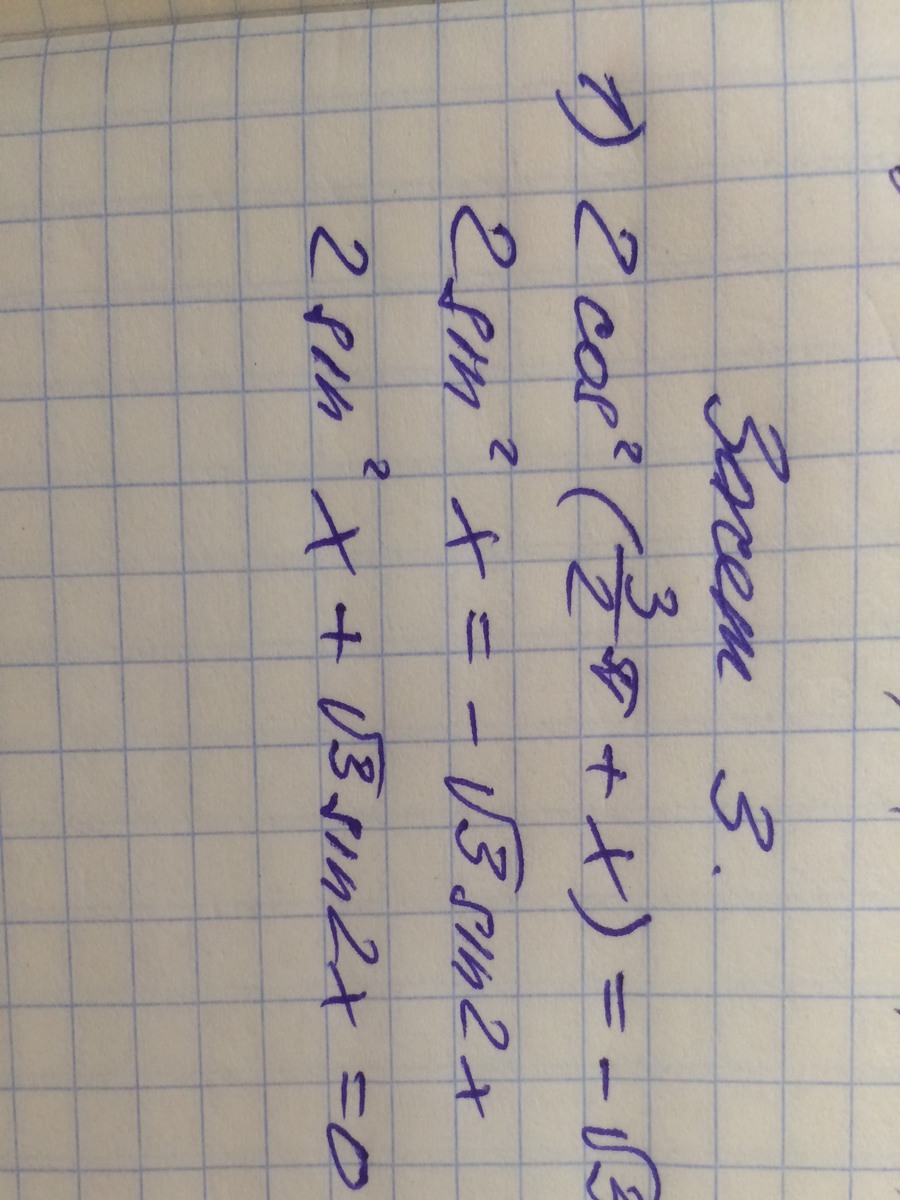
Ответы
Автор ответа:
0
Решение
2sin²x + √3 * sin2x = 0
2sin²x + √3 * 2sinxcosx = 0
2sinx*(sinx + √3cosx) = 0
1) sinx = 0
x₁ = πk, k ∈ Z
2) sinx + √3cosx = 0 делим на cosx ≠ 0
tgx + √3 = 0
tgx = - √3
x = arctg(- √3) + πn, n ∈ Z
x₂ = - π/3 + πn, n ∈ Z
Ответ: x₁ = πk, k ∈ Z ; x₂ = - π/3 + πn, n ∈ Z
2sin²x + √3 * sin2x = 0
2sin²x + √3 * 2sinxcosx = 0
2sinx*(sinx + √3cosx) = 0
1) sinx = 0
x₁ = πk, k ∈ Z
2) sinx + √3cosx = 0 делим на cosx ≠ 0
tgx + √3 = 0
tgx = - √3
x = arctg(- √3) + πn, n ∈ Z
x₂ = - π/3 + πn, n ∈ Z
Ответ: x₁ = πk, k ∈ Z ; x₂ = - π/3 + πn, n ∈ Z
Похожие вопросы
Предмет: История,
автор: s358974105655579
Предмет: Физика,
автор: xenia987
Предмет: Русский язык,
автор: arai27com
Предмет: Математика,
автор: Malinalove17
Предмет: Математика,
автор: jdjdgggd