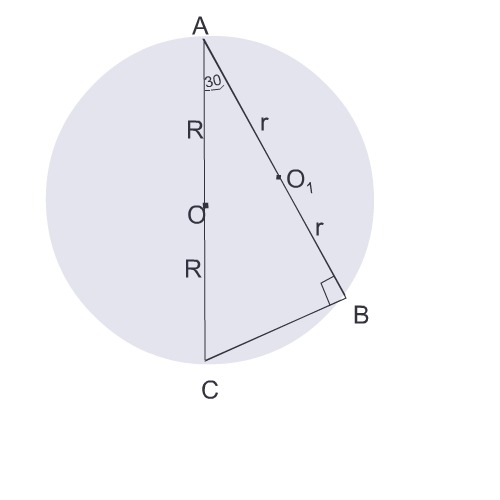
Площадь сечения шара плоскостью, проведенной через конец диаметра под углом 30 градусов к нему, равна 75п см^2. Найти диаметр шара.
Ответы
На данном Вами рисунке треугольник АОО1 - равнобедренный прямоугольный. Углы при диаметре сечения в рисунке равны. Обойдемся без него.
------------------------------------------------------------------------------
Смотрим на схематический рисунок, данный во вложении к задаче.
АС- диаметр шара и равен двум его радиусам.
АВ- диаметр сечения, также равен двум радиусам сечения.
Диаметр шара можно определить из прямоугольного треугольника АВС, где угол В - прямой, т.к угол АВС опирается на диаметр АС,
АС - гипотенуза, и
АВ - больший катет этого треугольника.
Так как угол САВ равен 30°, диаметр АС шара равен диаметру АВ сечения, деленному на косинус 30 градусов.
Диаметр сечения равен двум радиусам, которые можно найти из площади этого сечения.
S=πr²
r²=S:π
r²= 75 π:π=75 см²
r= 5√3 см
Диаметр АВ сечения =2r =10√3 см
АС=АВ:cos( 30°) =10√3:{(√3):2}=20√3):√3=20 см