Question

НАЙДИТЕ ТОЧКУ МАКСИМУМА ФУНКЦИИ
y=11+6√x-2x√x

Answer 1

y=11+6√x-2x√x     D(f)=x∈(0:+∞)

2x√x=2*x¹*x¹/₂=2*x³/²

6√x=6*x¹/²

f(x)=-2*x³/²+6*x¹/²+11

(2*x³/²)`=3*x¹/²=3√x

(6*x¹/²)`=3/x¹/²=3/√x

(11)`=0

f`(x)=-3√x+3/√x

    Приравниваем производную к нулю:

-3√x+3/√x=0

-3√x*√х+3=0

-3х+3=0

-3х=-3

х=1 - критическая точка.

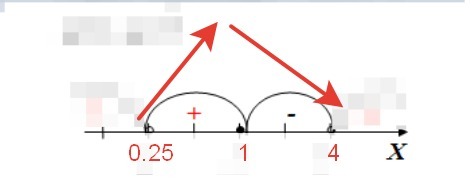
   Чтобы узнать, достигает ли функция максимума в точке экстремума х=1, нужно определить знаки производной методом интервалов (рисунок во вложении):

f`(1)=0

f`(0.25)=-3√0.25+3/√0.25=4.5>0 - функция возрастает на отрезке (0;1)

f`(4)=-3√4+3/√4=-4.5<0 - функция убывает на отрезке (1;+∞)

При переходе через точку х=1 производная меняет знак с "+" на "-", значит х=1 - точка максимума функции.