Question

В треугольника ABC угол A равен 40 градусам, угол C равен 60 градусам, BD-биссектриса, E-такая точка на AB, что BE=BC. Найдите угол ADE.

Answer 1

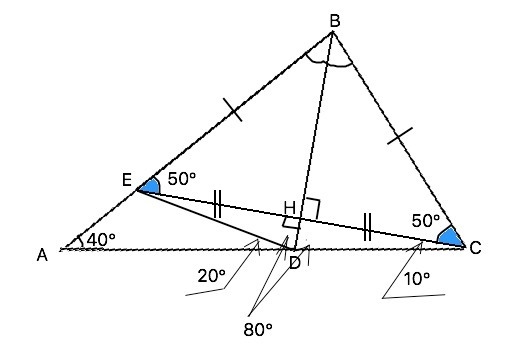
   Из суммы углов треугольника в треугольнике АВС угол В=180°- ∠А-∠С=80°. По условию ВЕ=ВС ⇒ ∆ ВЕС равнобедренный, поэтому биссектриса ВН, принадлежащая прямой ВD, является его медианой и высотой. Прямоугольные Δ ВЕН =Δ ВСН, их углы при вершине В равны 80:2=40°, углы при основании ЕС равны по (180°-80°):2= 50°. Отсюда  ∠НСD=60°-50°=10°. Угол СDH=180°- 90°-10°=80°. ∠НDA=180°-80°=100° ( смежный). В треугольнике СЕD точка Н - середина СЕ, ∠ЕНD=90° ⇒ HD - биссектриса угла D. ∠ВDЕ=80°, поэтому ∠АDE=∠АDH-∠EDH=100°-80°=20°.