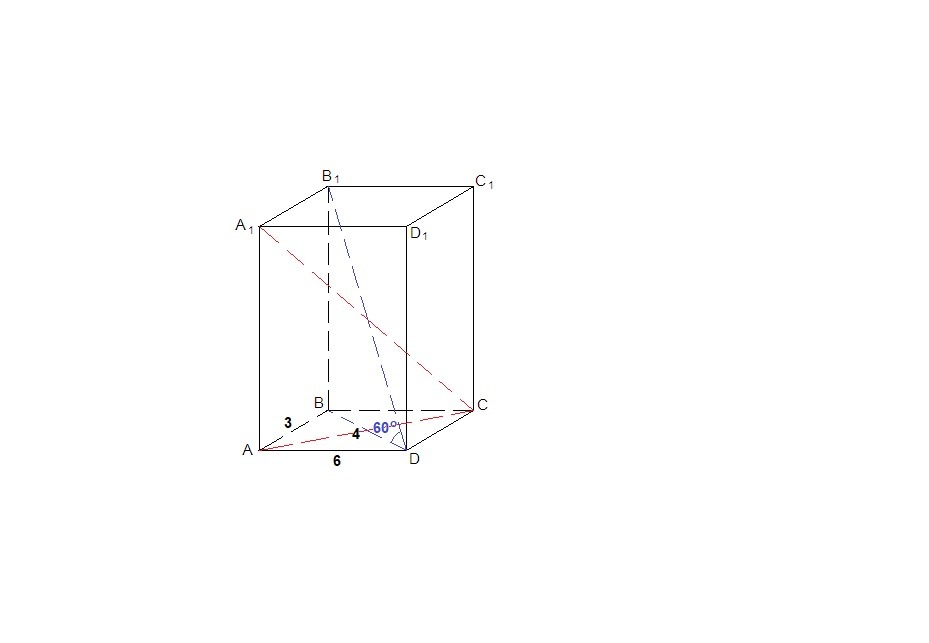
В прямоугольном параллелепипеде стороны основания 3 и 6 см, а одна из диагоналей основания 4 см. Найдите большую диагональ параллелепипеда, зная, что
меньшая диагональ образует с плоскостью основания угол 60º
ПОМОГИТЕ С РИСУНКОМ
Ответы
В условии, очевидно, ошибка: в прямоугольном параллелепипеде все грани прямоугольники, но тогда в прямоугольном треугольнике ABD гипотенуза (BD = 4 см) меньше катета (АD = 6 см).
Вероятно, в задаче дан прямой параллелепипед. Тогда его основания - параллелограммы, а боковые грани - прямоугольники. Решим задачу для прямого параллелепипеда.
Итак, в основании параллелограмм, в котором
АВ = CD = 3 см,
BC = AD = 6 см,
BD = 4 см - меньшая диагональ параллелограмма.
Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон:
AC² + BD² = 2(AB² + AD²)
AC² = 2(AB² + AD²) - BD² = 2(9 + 36) - 16 = 90 - 16 = 74
AC = √74 см
B₁D - меньшая диагональ параллелепипеда (так как ее проекция меньше).
ΔBB₁D: ∠B₁BD = 90°,
tg∠BDB₁ = BB₁ / BD
BB₁ = BD · tg60° = 4 · √3 = 4√3 см
АА₁ = ВВ₁ = 4√3 см
ΔAA₁C: ∠A₁AC = 90°, по теореме Пифагора
A₁C = √(AA₁² + AC²) = √(48 + 74) = √122 см