Предмет: Математика,
автор: Вaлерьянка
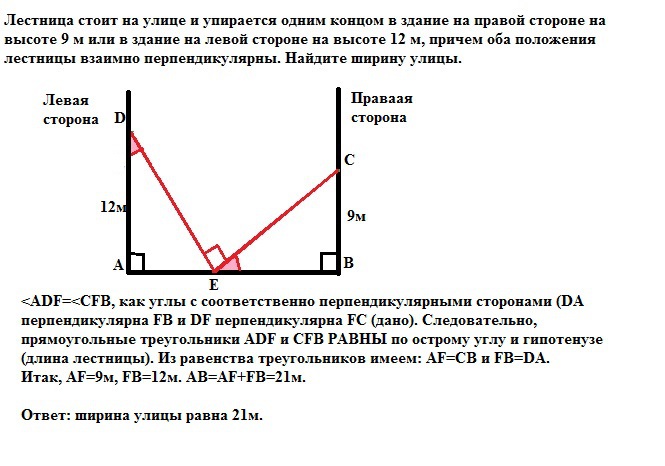
Лестница стоит на улице и упирается одним концом в здание на правой стороне на высоте 9 м или в здание на левой стороне на высоте 12 м, причем оба положения лестницы взаимно перпендикулярны. Найдите ширину улицы.
Ответы
Автор ответа:
0
Обозначим концы лестницы буквами Е и С когда она прислонена к стене на правой стороне улицы, а буквами Е и D - когда прислонена к стене на левой стороне.
<ADЕ=<CЕB, как углы с соответственно перпендикулярными сторонами (DA перпендикулярна ЕB и DЕ перпендикулярна ЕC (дано). Следовательно, прямоугольные треугольники ADЕ и CЕB РАВНЫ по острому углу и гипотенузе (длина лестницы). Из равенства треугольников имеем: АЕ=CB и ЕB=DA.
Итак, AЕ=9м, ЕB=12м. АВ=АЕ+ЕB=21м.
Ответ: ширина улицы равна 21м.
<ADЕ=<CЕB, как углы с соответственно перпендикулярными сторонами (DA перпендикулярна ЕB и DЕ перпендикулярна ЕC (дано). Следовательно, прямоугольные треугольники ADЕ и CЕB РАВНЫ по острому углу и гипотенузе (длина лестницы). Из равенства треугольников имеем: АЕ=CB и ЕB=DA.
Итак, AЕ=9м, ЕB=12м. АВ=АЕ+ЕB=21м.
Ответ: ширина улицы равна 21м.
Приложения:
Похожие вопросы
Предмет: Математика,
автор: foswas
Предмет: Английский язык,
автор: kotenek1985
Предмет: Английский язык,
автор: kiselevad373
Предмет: Математика,
автор: musicmusic2011