Предмет: Алгебра,
автор: Аноним
СРОЧНО!! 100 БАЛЛОВ!! Надо дорешать задачу! Вычислите площадь фигуры ограниченной линиями  ,
,  ,
,  . Надо ещё начертить график!
. Надо ещё начертить график!
Приложения:
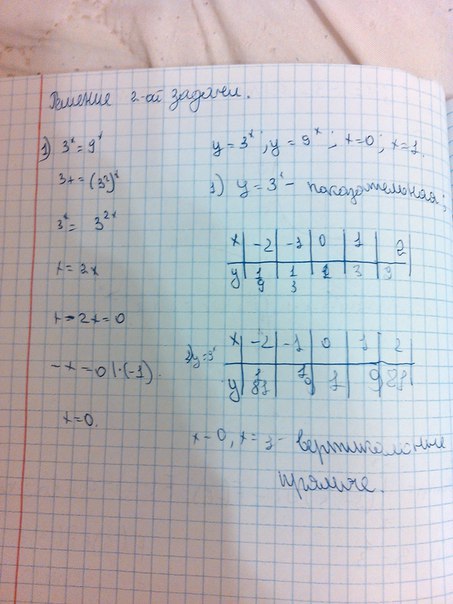
Ответы
Автор ответа:
0
Находим точки пересечения графиков:
3ˣ=9ˣ
3ˣ=3²ˣ
х=2х
х=0
Поулчаем пределы интегрирования
х=0, второе значение х=1 - дано

3ˣ=9ˣ
3ˣ=3²ˣ
х=2х
х=0
Поулчаем пределы интегрирования
х=0, второе значение х=1 - дано
Автор ответа:
0
Найдем отрезок на котором определенна фигура.
Для этого сравним 2 функции.




Последняя граница нам уже дана.
Поэтому имеем отрезок:
![[0,1] [0,1]](https://tex.z-dn.net/?f=%5B0%2C1%5D)
Отсюда определенный интеграл:


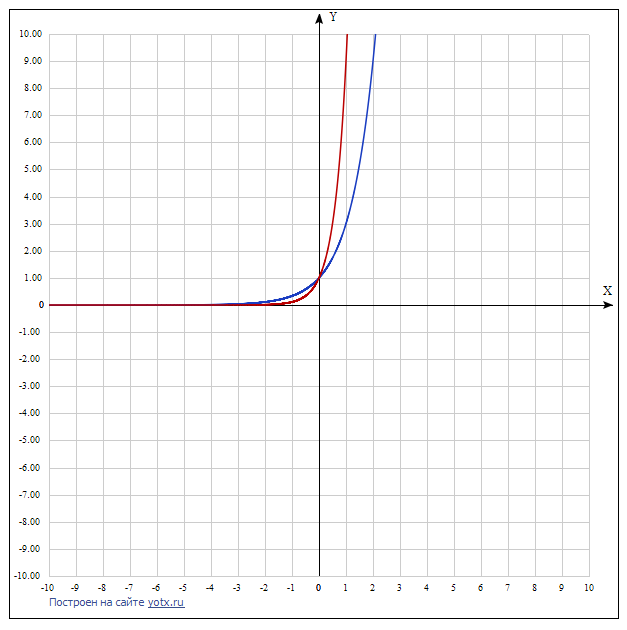
График во вложении.
P.S.
Красный график
Для этого сравним 2 функции.
Последняя граница нам уже дана.
Поэтому имеем отрезок:
Отсюда определенный интеграл:
График во вложении.
P.S.
Красный график
Приложения:
Похожие вопросы
Предмет: Химия,
автор: gerey06
Предмет: Русский язык,
автор: klikerradrigis54
Предмет: Экономика,
автор: kristinka0695
Предмет: Физика,
автор: Аноним
Предмет: География,
автор: novositi