Предмет: Геометрия,
автор: maksim99997336
Начертите треугольник ABC. Постройте его образ:
а) при симметрии относительно его высоты, выходящей из вершины А;
б) при симметрии относительно точки D, являющейся серединой стороны AB;
в)при параллельном переносе на вектор AM, где M - точка пересечения медиан треугольника;
г)при повороте вокруг вершины С на 45 градусов против часовой стрелки.
Ответы
Автор ответа:
0
а) Пусть АН - высота треугольника, она же ось симметрии.
Так как вершина А лежит на оси симметрии, она отобразится в себя (т.е. точка А' совпадет с А).
Чтобы отобразить точку В относительно оси АН, надо построить из точки В луч, перпендикулярный АН, а это и есть прямая ВС.
Затем на луче ВН откладываем отрезок НВ', равный ВН, по другую сторону от точки Н.
На луче СН по другую сторону от точки Н откладываем отрезок НС', равный СН.
ΔA'B'C' - искомый.
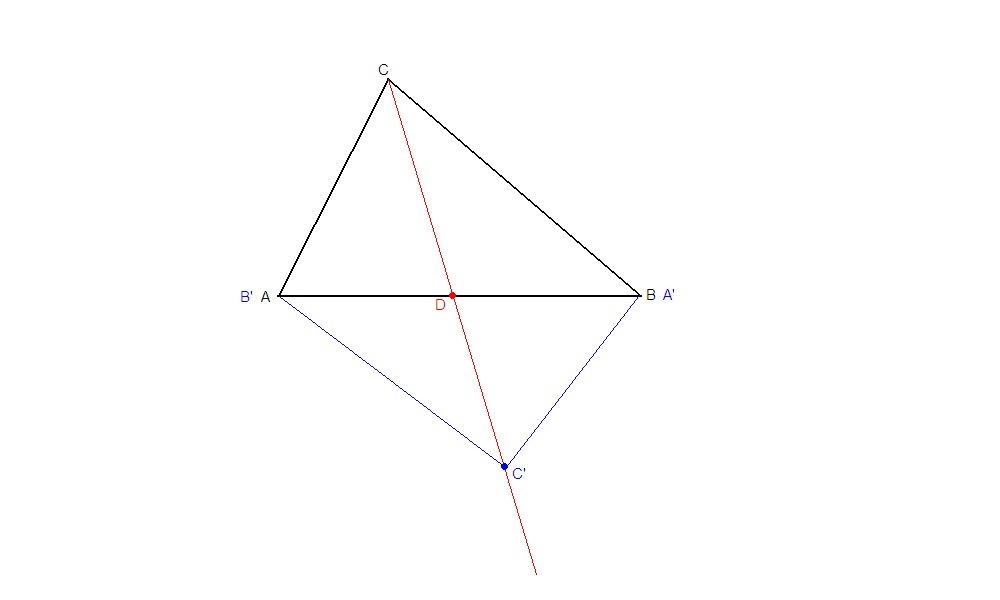
б) Пусть D - середина АВ.
Проводим луч CD, на котором откладываем отрезок CA' = CD.
На луче AD откладываем отрезок DA' = AD. Так как D - середина АВ, точка A' совпадет с точкой В.
На луче BD откладываем отрезок DB' = BD. Так как D - середина АВ, точка В' совпадет с точкой А.
ΔA'B'C' - искомый.
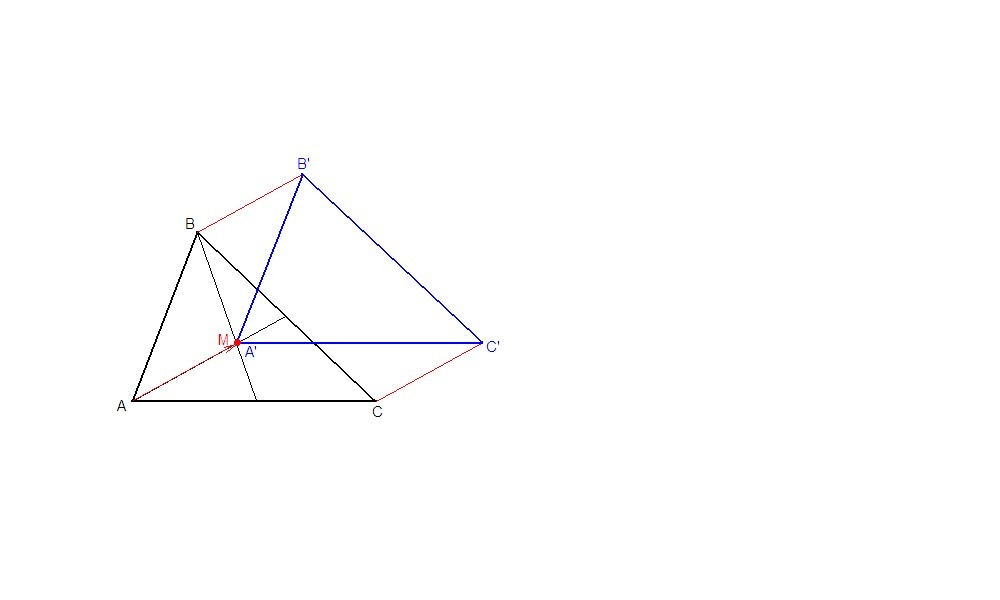
в) М - точка пересечения медиан треугольника АВС.
Из вершин А, В и С проводим лучи, параллельные АМ. На них откладываем отрезки AA', BB' и CC', равные длине отрезка АМ.
При этом точка А' совпадет с точкой М.
ΔA'B'C' - искомый.
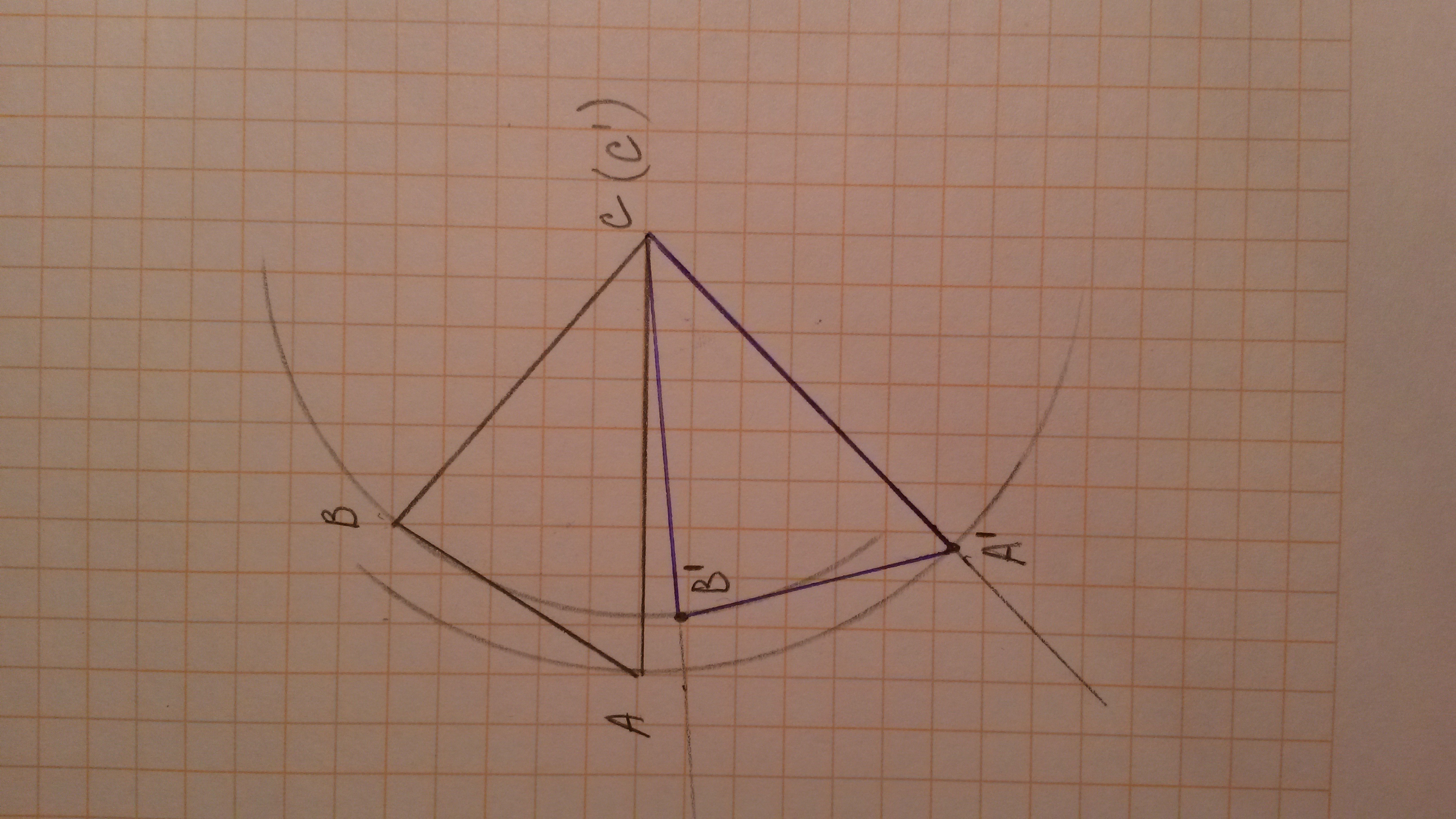
г) Так как С - центр поворота, то точка С отобразится на себя.
Строим окружность с центром в точке С и радиусом ВС.
Строим угол, равный 45° с вершиной в точке С и стороной ВС (против часовой стрелки). Точка пересечения окружности и второй стороны угла - точка В'.
Строим окружность с центром в точке С и радиусом АС.
Строим угол, равный 45° с вершиной в точке С и стороной АС (против часовой стрелки). Точка пересечения окружности и второй стороны угла - точка А'.
ΔA'B'C' - искомый.
Так как вершина А лежит на оси симметрии, она отобразится в себя (т.е. точка А' совпадет с А).
Чтобы отобразить точку В относительно оси АН, надо построить из точки В луч, перпендикулярный АН, а это и есть прямая ВС.
Затем на луче ВН откладываем отрезок НВ', равный ВН, по другую сторону от точки Н.
На луче СН по другую сторону от точки Н откладываем отрезок НС', равный СН.
ΔA'B'C' - искомый.
б) Пусть D - середина АВ.
Проводим луч CD, на котором откладываем отрезок CA' = CD.
На луче AD откладываем отрезок DA' = AD. Так как D - середина АВ, точка A' совпадет с точкой В.
На луче BD откладываем отрезок DB' = BD. Так как D - середина АВ, точка В' совпадет с точкой А.
ΔA'B'C' - искомый.
в) М - точка пересечения медиан треугольника АВС.
Из вершин А, В и С проводим лучи, параллельные АМ. На них откладываем отрезки AA', BB' и CC', равные длине отрезка АМ.
При этом точка А' совпадет с точкой М.
ΔA'B'C' - искомый.
г) Так как С - центр поворота, то точка С отобразится на себя.
Строим окружность с центром в точке С и радиусом ВС.
Строим угол, равный 45° с вершиной в точке С и стороной ВС (против часовой стрелки). Точка пересечения окружности и второй стороны угла - точка В'.
Строим окружность с центром в точке С и радиусом АС.
Строим угол, равный 45° с вершиной в точке С и стороной АС (против часовой стрелки). Точка пересечения окружности и второй стороны угла - точка А'.
ΔA'B'C' - искомый.
Приложения:

Похожие вопросы
Предмет: Химия,
автор: Badabex
Предмет: Физика,
автор: Аноним
Предмет: Қазақ тiлi,
автор: Аноним
Предмет: Математика,
автор: jijiloliza
Предмет: Литература,
автор: Davydovalizka