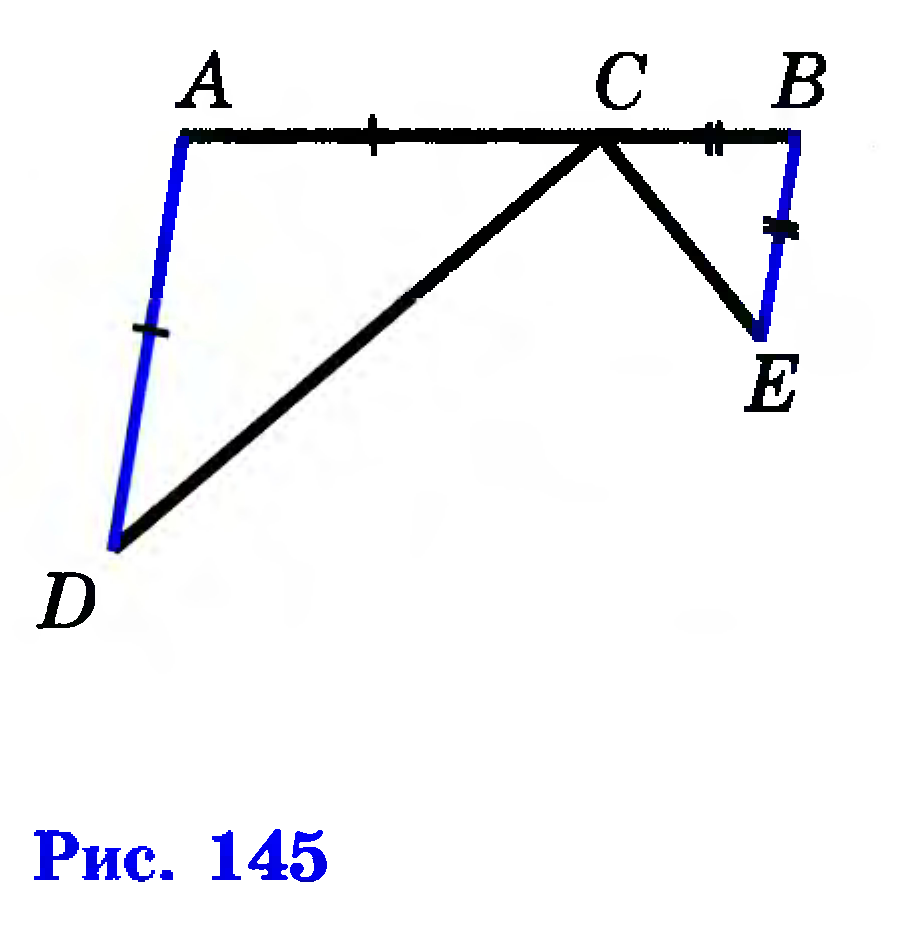
Помогите пожалуйста! Очень нужно! На рисунке 145. (Он ниже) AD||BE, AC=AD и BC=BE. Докажите, что угол DCE-прямой.
Ответы
Продлеваем сторону АД и сторону СЕ - точка соединения Н, получаем треугольник ДНС
Продлеваем ЕВ и ДС до соединения получаем точку М и треугольник ЕСМ
Угол СЕВ= углу ВСЕ , треугольник СВЕ равнобедренный
угол АДС=углу АСД, треугольник АСД равнобедренный
Угол АДС = углу СМВ как внутренние разносторонние
Угол АДС= углу ВСМ как вертикальные, треугольник СМВ равнобедренный угол МСВ=углу СМВ, отсюда СВ=ВМ=ВЕ, т.е СВ - медиана треугольника СЕМ и равна 1/2ЕМ.
Такое соотношение когда медиана = 1/2 стороны которую она делит возможно только в прямоугольном треугольнике. Значит угол МСЕ=90
Угол МСЕ=углу ДСН как вертикальные = 90, угол НСМ=углу ДСЕ как вертикальные и =
=(360 -90-90)/2=90