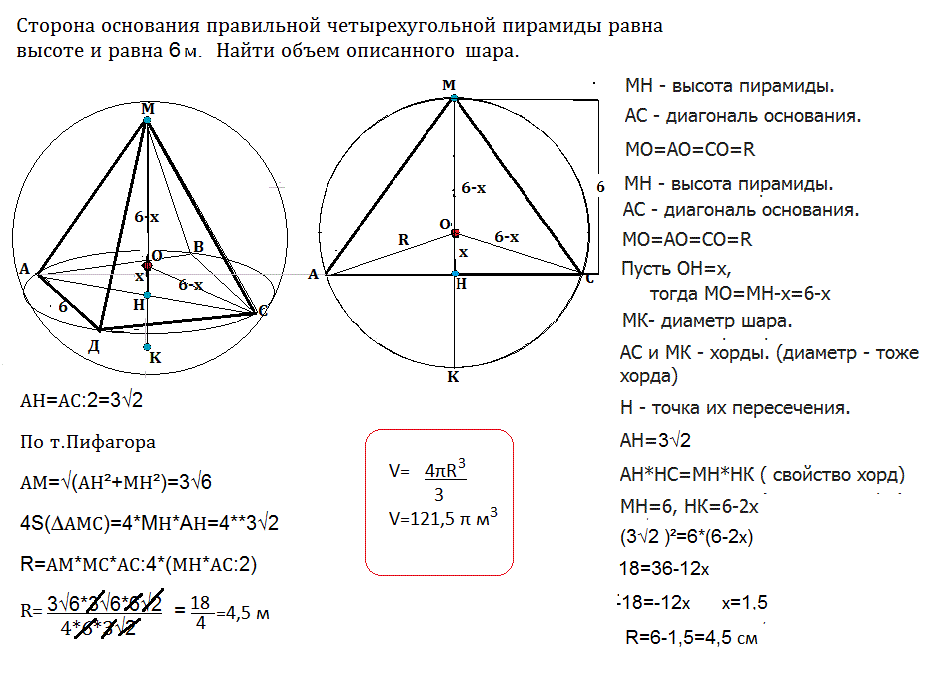
Стороны основания правильной четырехугольной пирамиды равна высоте и равна 6 М. Найти объем описанного шара.
Ответы
Сторона основания правильной четырехугольной пирамиды равна высоте и равна 6 м. Найти объем описанного шара.
V =4 *π *R³/3
R=?
V=?
R = радиусу окружности, описанной около равнобедренного треугольника с боковыми сторонами, равными боковым ребрам пирамиды, и основанием, равным диагонали основания пирамиды.
Способ 1 нахождения радиуса описанного шара
Радиус описанной окружности
R=a*b*c:4S=АМ*МС*АС:4*(МН*АС:2)
АС- диагональ основания и по свойству диагонали квадрата равна АB*√2=6√2
АН=АС:2=3√2
По т.Пифагора
АМ=√(АН²+МН²)=3√6
4S(∆АМС)=4*MН*AН=4*6*3√2
R=АМ*МС*АС:4*(МН*АС:2)=18/4=4,5 м
-------------
Способ 2 нахождения радиуса шара (см.рисунок).
МН - высота пирамиды.
АС - диагональ основания.
МО=AO=CO=R
Пусть ОН=х, тогда
МО=МН-х=6-х
МК- диаметр шара.
АС и МК - хорды. (диаметр - тоже хорда)
Н - точка их пересечения.
АН=3√2 (см. выше)
АН*НС=МН*НК ( свойство хорд)
МН=6, НК=6-2х
(3√2 )²=6*(6-2х)
18=36-12х
-18=-12х
х=1,5
R=6-1,5=4,5 м
--------------
V=4*π*(4,5)³:3
V=121,5π или ≈381,7 (π -полностью по калькулятору)
Если брать π=3,14, то
V=381,51. Разница довольно существенная.