Предмет: Алгебра,
автор: Nik133
Решить диференциальное уравнение
Ответы
Автор ответа:
0
Смотрите решение во вложениях
Приложения:
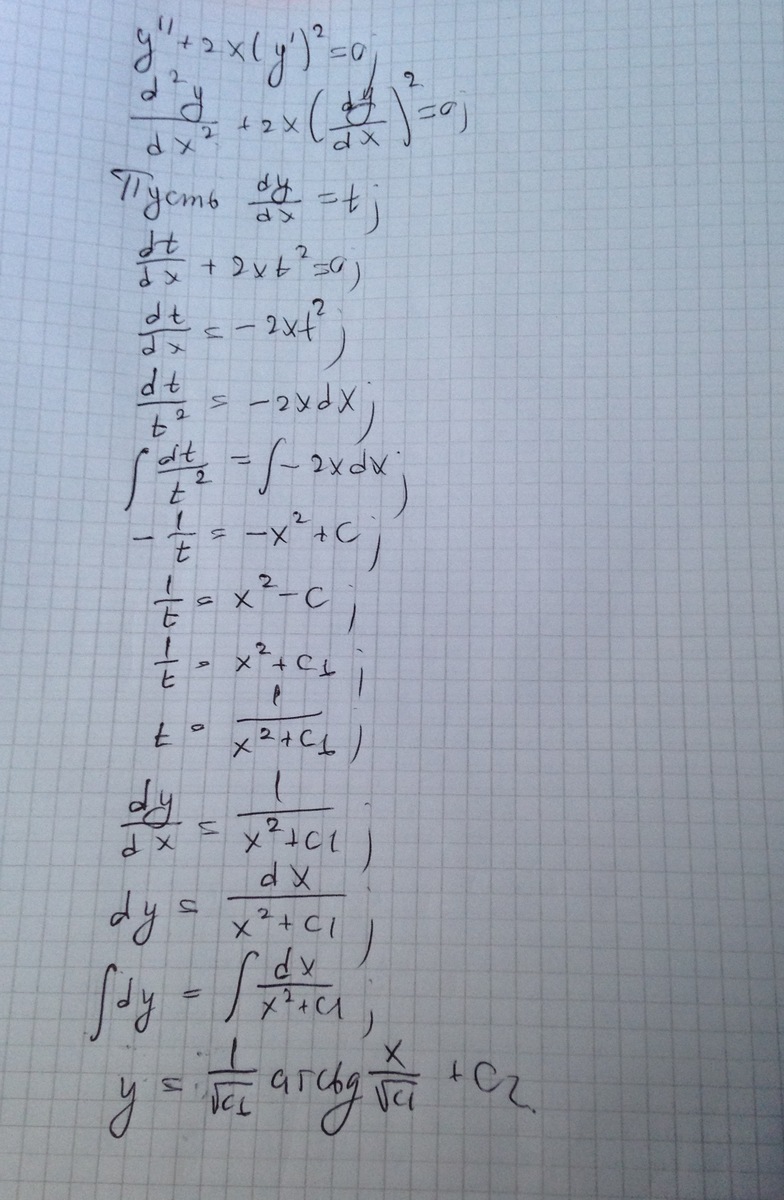
Автор ответа:
0
Замена:у¹=p(x), y¹¹=p¹(x)=dp/dx
p¹+2xp²=0, dp/dx=-2xp², ∫dp/p²=-2∫xdx, -1/p=-x²+C₁, 1/p=x²+C₁
p=1/(C₁+x²), dy/dx=1/(C₁+x²), ∫dy=∫dx/(C₁+x²), ∫dy=∫dx/(x²+C₁)
y=1/C * aratgx/C +C₂, где обозначили √C₁=C.
Приложения:
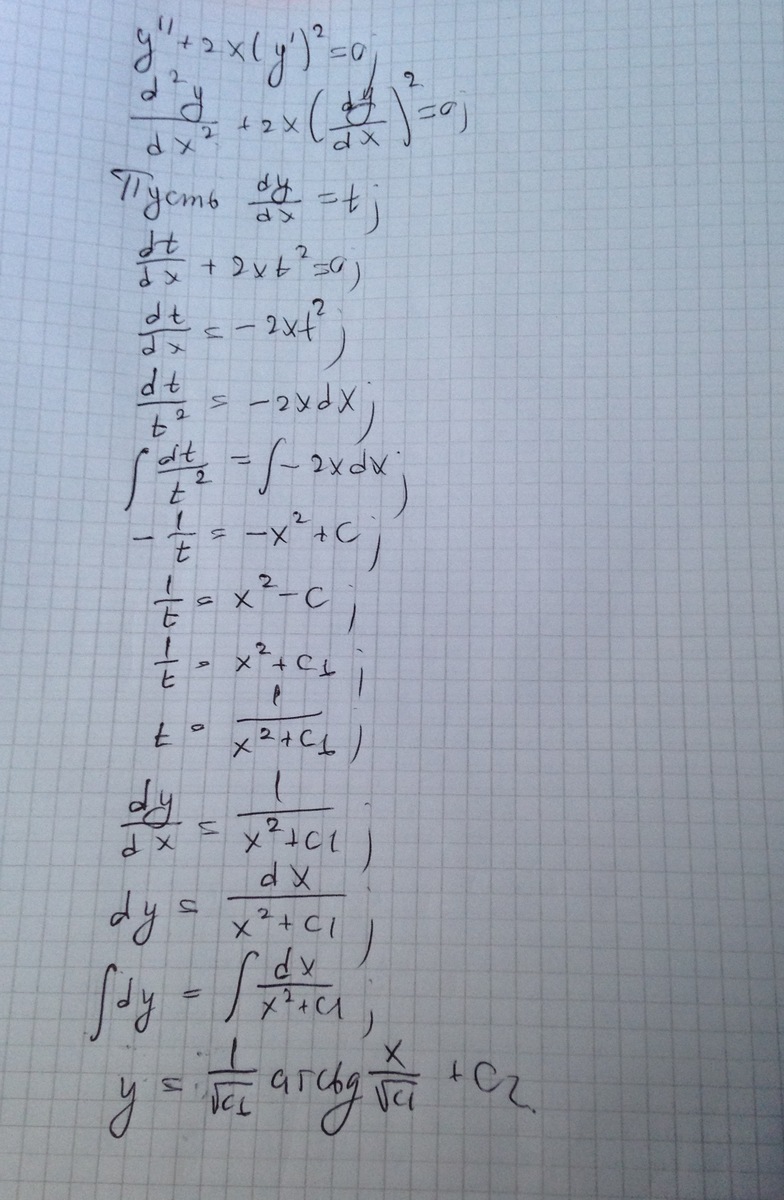
Похожие вопросы
Предмет: Другие предметы,
автор: atalipov731
Предмет: Русский язык,
автор: asetkyzydiana2009
Предмет: Математика,
автор: ShaikenAlmira
Предмет: Математика,
автор: Milllove