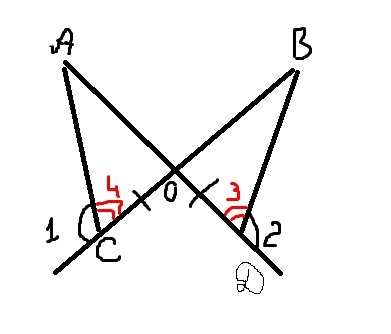
Лучи AD и BC пересекаются в точке O, угол 1 = углу 2, OC = OD. Докажите, что OA = OB.
Ответы
Рассмотрим ΔАОС и ΔВОD.
∠АОС = ∠ВОD как вертикальные.
∠АСО является смежным углу 1.
∠ВDО является смежным углу 2.
Поскольку ∠1=∠2 (по условию), то и ∠АСО = ∠ВDО.
СО = ОD по условию.
ΔАОС = ΔВОD по стороне и двум прилежащим к ней углам.
В равных треугольниках соотвествующие элементы равны.
Значит АО = ОВ.
Что и требовалось доказать.
Внешние углы 1 и 2 равны, тогда внутренние углы 3 и 4 тоже равны.
∠ AOC = ∠ BOD как вертикальные.
По второму признаку равенства треугольников, если одна сторона и прилежащие к ней углы одного треугольника равны соответственно стороне и прилежащим к ней углам другого треугольника то такие треугольники равны, т.е. Δ AOC = Δ BOD из этого вытекает,что стороны AO = OB