Предмет: Алгебра,
автор: Physic79832
Как доказать в 31.20 помогите не понимаю сути
Приложения:
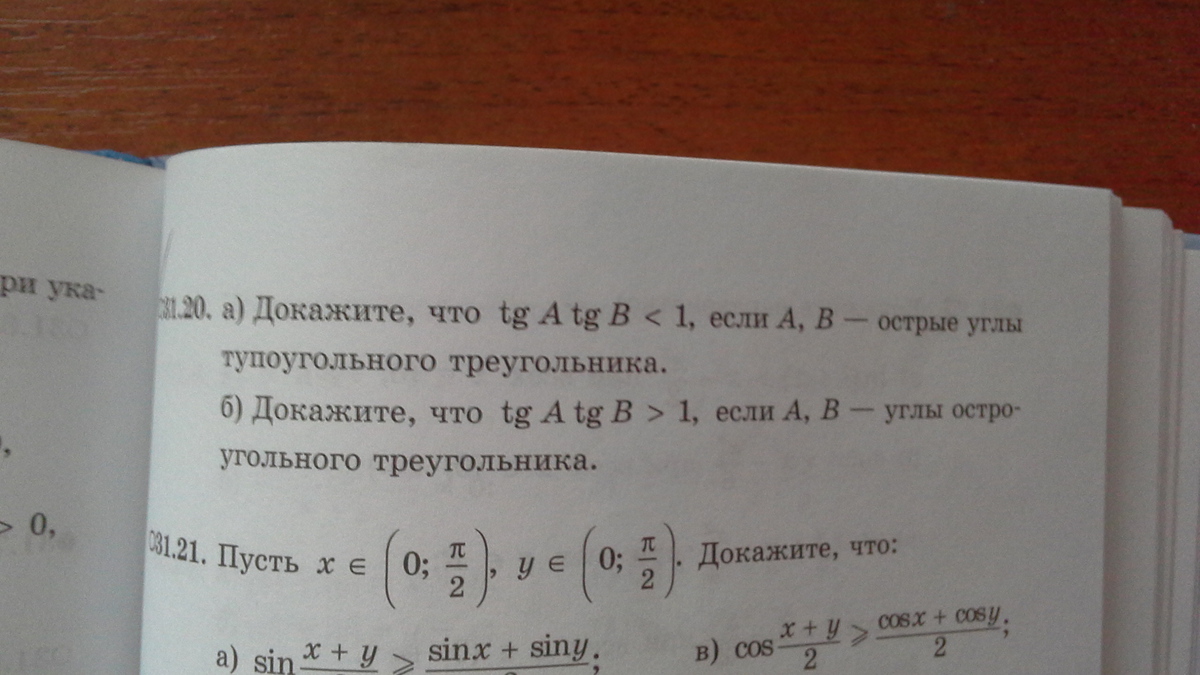
Ответы
Автор ответа:
0
1)
A, B -острые, С -тупой. A+B = 180-C
Это значит: 0<A<90; 0<B<90; 90<C<180
cosA>0 cosB>0 cosC<0
tgA*tgB <1 ----> tgA*tgB -1<0 (1)
( формулы: tgx=sinx/cosx
cos(180-A)= - cos(A)
cos(A+B) =cosA*cosB - sinA*sinB )
преобразуем (1) :
tgA*tgB -1 = (sinA *sinB)/(cosA*cosB) -1=
=(sinA*sinB -cosA*cosB)/(cosA*cosB) = - cos(A+B)/(cosA*cosB)=
= cos(180-(A+B))/(cosA*cosB) =cosC/(cosA*cosB) <0,
а это значит: tgA*tgB -1<0 или tgA*tgB < 1
2) делается аналогично, только там
cosA>0 cosB>0 cosC>0 и так далее и в конце
рассуждений получается соsC/(cosA*cosB) > 0 и вывод:
tgA*tgB -1>0 или tgA*tgB>1
A, B -острые, С -тупой. A+B = 180-C
Это значит: 0<A<90; 0<B<90; 90<C<180
cosA>0 cosB>0 cosC<0
tgA*tgB <1 ----> tgA*tgB -1<0 (1)
( формулы: tgx=sinx/cosx
cos(180-A)= - cos(A)
cos(A+B) =cosA*cosB - sinA*sinB )
преобразуем (1) :
tgA*tgB -1 = (sinA *sinB)/(cosA*cosB) -1=
=(sinA*sinB -cosA*cosB)/(cosA*cosB) = - cos(A+B)/(cosA*cosB)=
= cos(180-(A+B))/(cosA*cosB) =cosC/(cosA*cosB) <0,
а это значит: tgA*tgB -1<0 или tgA*tgB < 1
2) делается аналогично, только там
cosA>0 cosB>0 cosC>0 и так далее и в конце
рассуждений получается соsC/(cosA*cosB) > 0 и вывод:
tgA*tgB -1>0 или tgA*tgB>1
Автор ответа:
0
объясните пожалуйста подробно и для 2 случая у меня -cosx получается
Автор ответа:
0
вычисления те же самые, только знак у cosC>0 !!!!!
Похожие вопросы
Предмет: Русский язык,
автор: dzojenruslan
Предмет: Немецкий язык,
автор: drahmanina759
Предмет: Химия,
автор: Аноним
Предмет: Математика,
автор: yorf