Question

Срочно!! SOSs!! Пожалуйста !! Задание 3 и 4!!Перевод : 3) в нижнем основании цилиндра проведена хорда которая находиться на расстояние d


От центра верхнего основания , которую видно из этого центра под углом фи


От резок который получает центр верхнего основание с точкой окружности нижнего основания


Создают с плоскостью нижнего основания угол бетта найти объем цилиндра


4) основанием пирамиды - ромб со стройной 16 см и острым углом 60


Все двухраненые углы при основании пирамиды раны 30 найти объем конуса


вписанного в данную пирамиду

Answer 1

Осмелюсь дополнить.
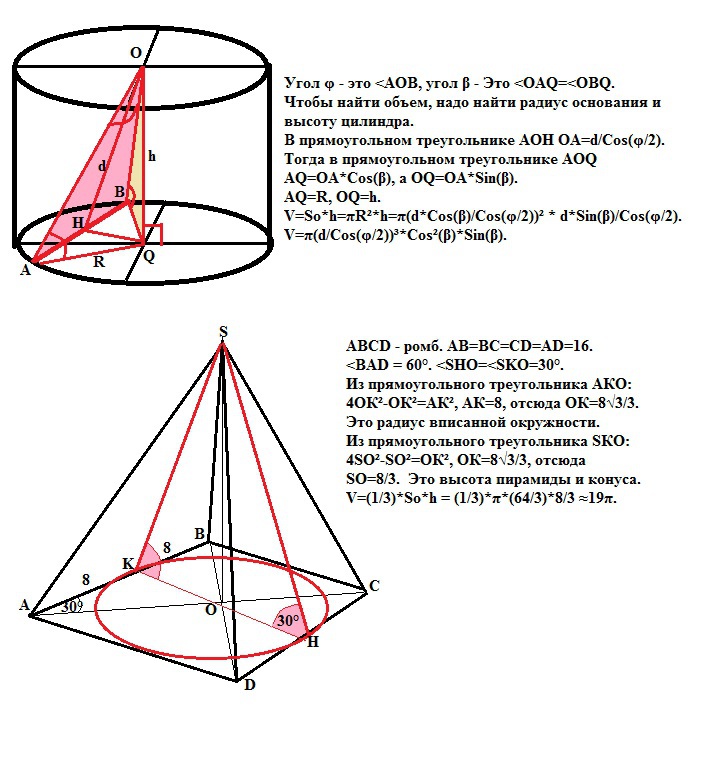
3). Угол φ - это <AOB, угол β - Это <OAQ=<OBQ.
Чтобы найти объем, надо найти радиус основания и высоту цилиндра.
В прямоугольном треугольнике АОН OA=d/Cos(φ/2).
Тогда в прямоугольном треугольнике АОQ АQ=OA*Cos(β), а ОQ=ОА*Sin(β).
AQ=R, OQ=h. V=So*h=πR²*h=π(d*Cos(β)/Cos(φ/2))² * d*Sin(β)/Cos(φ/2).
V=π(d/Cos(φ/2))³*Cos²(β)*Sin(β).
4).АВСD - ромб. АВ=ВС=СD=AD=16.
<BAD = 60°. <SHO=<SKO=30°.
Из прямоугольного треугольника АКО:
4ОК²-ОК²=АК², АК=8, отсюда ОК=8√3/3.
Это радиус вписанной окружности.
Из прямоугольного треугольника SКО:
4SO²-SО²=OК², ОК=8√3/3, отсюда
SО=8/3.  Это высота пирамиды и конуса.
V=(1/3)*So*h = (1/3)*π*(64/3)*8/3 ≈18,96π=19π.