Помогите решить задачу .
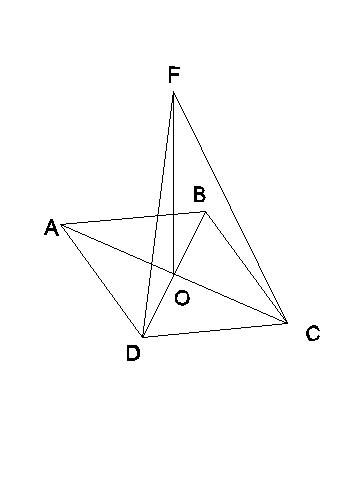
Диагонали ромба ABCD пересекаются в точке О, отрезок OF перпендикулярен плоскости ромба.вычислите длины диагоналей ромба, если FC=7 см , FD=5 см, а площадь ромба равна 16 квадратных сантиметров .
Ответы
Обозначим диагонали ромба - d1 и d2.
Площадь ромба S =( d1 * d2) / 2 = 16 cm^2, 2 * 16 = d1 * d2 или d1 = 32 / d2.
Из прямоугольных треугольников FOC и FOD следует - (у них общая высота):
5^2 - (d1/2)^2 = 7^2 -(d2/2)^2. Приведя к общему знаменателю, получим:
100 - d1^2 = 196 - d2^2 или d2^2 - d1^2 = 96. Подставив в это уравнение значение
d1 = 32 / d2, получим: d2^2-(32 / d2)^2 = 96.Примем d2^2 за "х", уравнение примет вид
x^2 - 96x -1024 = 0 x = 48 +- V(48^2 + 1024) x1 = 55.595 x2 = 40.405. Извлекая корень квадратный их этих значений, получаем:
d2(1) = 7.456 cm d2(2) = 6.356 cm
d1(1) = 4.292 cm d1(2) = 5.034 cm.