Предмет: Математика,
автор: Аноним
В прямоугольном треугольнике высота опущенная на гипотенузу вчетверо короче гипотенузы. Найдите острые углы треугольника
Ответы
Автор ответа:
0
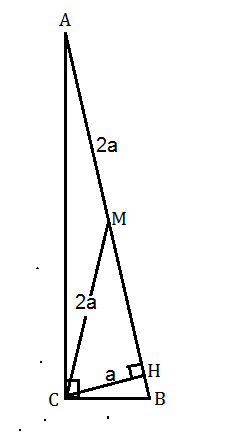
Обозначим вершины треугольника А. В, С. Угол С=90º
СН - высота, АВ - гипотенуза.
Пусть СН=а, тогда АВ=4а
Проведем медиану СМ. ⇒
АМ=МВ=2а
В прямоугольном ∆ МНС гипотенуза СМ=2а. ⇒
Катет СН=1/2 гипотенузы СМ, значит, ∠ НМС=30º
Смежный с ним угол СМА =180º-30º=150º
По свойству медианы прямоугольного треугольника СМ=АМ⇒
АМС - равнобедренный.
∠САМ=∠АСМ=(180º-150º):2=15º
В прямоугольном треугольнике сумма острых углов равна 90º
∠ СВА=90º -15º =75º
Ответ: 15°; 75°
СН - высота, АВ - гипотенуза.
Пусть СН=а, тогда АВ=4а
Проведем медиану СМ. ⇒
АМ=МВ=2а
В прямоугольном ∆ МНС гипотенуза СМ=2а. ⇒
Катет СН=1/2 гипотенузы СМ, значит, ∠ НМС=30º
Смежный с ним угол СМА =180º-30º=150º
По свойству медианы прямоугольного треугольника СМ=АМ⇒
АМС - равнобедренный.
∠САМ=∠АСМ=(180º-150º):2=15º
В прямоугольном треугольнике сумма острых углов равна 90º
∠ СВА=90º -15º =75º
Ответ: 15°; 75°
Приложения:
Похожие вопросы
Предмет: География,
автор: aleksmit96
Предмет: Физика,
автор: leem66946
Предмет: Алгебра,
автор: DOodldkd
Предмет: Математика,
автор: ketrin070902
Предмет: Математика,
автор: VNMKJH