Question

70 БАЛЛОВ.
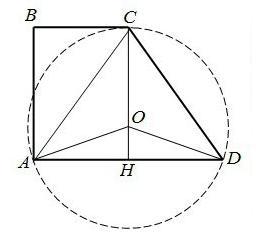
ABCD — прямоугольная трапеция с прямым углом А и меньшим основанием ВС=1. Окружность с центром в точке О касается прямой ВС в точке С и проходит через точки А и D, угол CDA=60° найдите длину CD

Answer 1

∠A = ∠B = 90°
AO = OC = OD (т.к. они являются радиусами окружности)
H - точка пересечения OC и AD, CH ⊥ AD.
ΔAOD - равнобедренный (AO = OD). OH - высота, биссектриса и медиана. Т.к. ОН - медиана, то AH = HD. AH = BC = HD = 1.
ΔHCD - прямоугольный, ∠DHC = 90°, ∠CDH = 60°
∠HCD + ∠DHC +  ∠CDH = 180°
∠HCD = 180° - 90° - 60°
∠HCD = 30°
Против угла в 30° лежит катет, равный половине гипотенузы. 
HD = 1/2 * CD 
CD = 2 * HD
CD = 2 * 1 = 2
Ответ: 2

Answer 2

  Проводим высоту СН. Точка О - центр окружности лежит на СН - прямая перпендикулярная в точке касания к окружности проходит через её центр.
  ВС=АН=1.
  AD - хорда окружности.
  АН=AD=1 - прямая из центра окружности перпендикулярная хорде делит её пополам.
  Из ΔСНD - ∠С=30° ⇒ СD=2*1=2 ед.