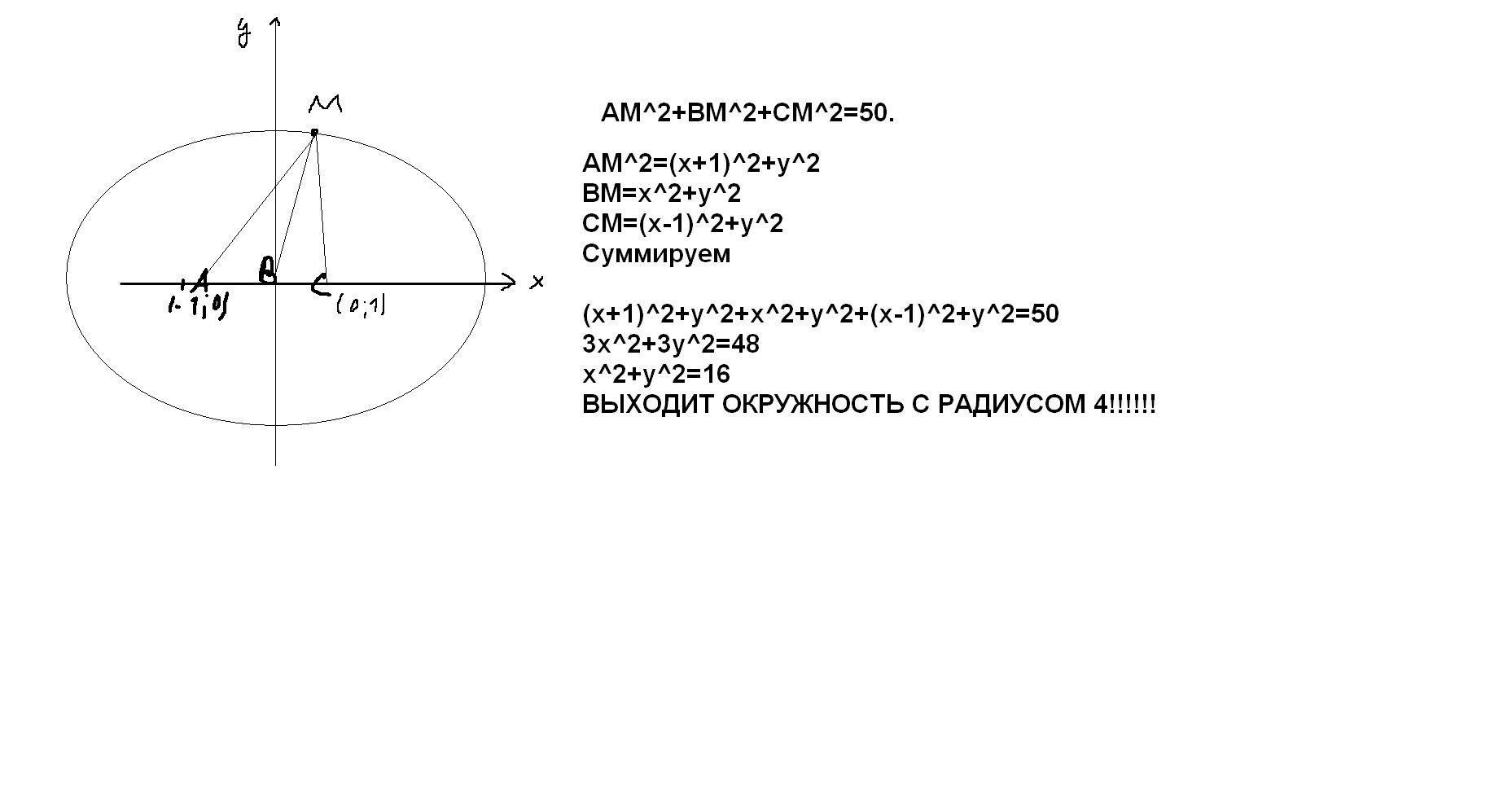
Точка В середина отрезка АС, длина которого равна 2. Найдите множество всех точек М, для каждой их которых: АМ^2+BM^2+CM^2=50. Помогите побыстрей. ооочень надо!
Ответы
поместим точку В в начало координат и напишем квадраты расстояния до точки М(xm,ym) от остальных точек
АМ^2=(xm+1)^2+ym^2
BM^2=xm^2+ym^2
CM^2=(xm-1)^2+ym^2
Сложим все эти величины, должно получиться 50
(xm+1)^2+ym^2+xm^2+ym^2+(xm-1)^2+ym^2=50
раскроем скобки
xm^2+2xm+1^2+ym^2+xm^2+ym^2+xm^2-2xm+1+ym^2=50
приведем подобные члены
3xm^2+3ym^2+2=50
3xm^2+3ym^2=48
xm^2+ym^2=16
xm^2+ym^2=4^2
Это уравнение окружности с центром в точке В и радиусом 4.
Множество точек М - окружность с радиусом 4 и центром в В. смотри рисунок
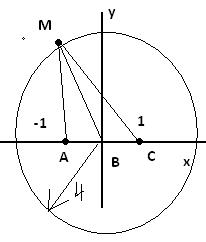
это видно что окружность так как МНОЖЕСТВО!
Представим это все в прямоугольной системе координат
где х и у