Предмет: Алгебра,
автор: MissKrash
помогите ,пожалуйста,номер 11
Приложения:
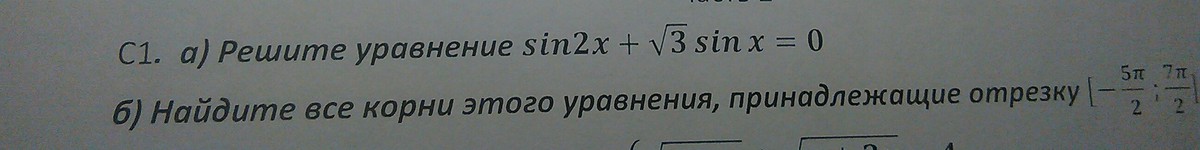
Ответы
Автор ответа:
0
Автор ответа:
0
спасибо большое !
Автор ответа:
0
Похожие вопросы
Предмет: Информатика,
автор: crycry1821
Предмет: История,
автор: Аноним
Предмет: Математика,
автор: dinaraymarova581
Предмет: Математика,
автор: nikulasenko
Предмет: Математика,
автор: Varganovavova