Предмет: Геометрия,
автор: ЛеонаАзалия
Срочно!! Спасите !!!
Приложения:

Ответы
Автор ответа:
0
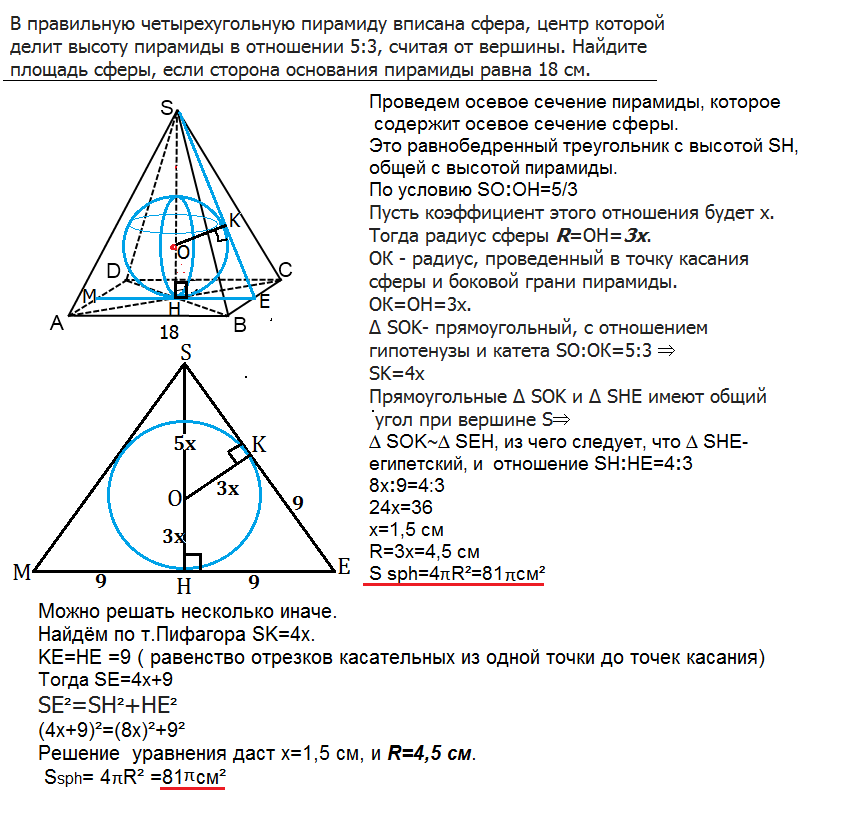
В правильную четырехугольную пирамиду вписана сфера, центр которой делит высоту пирамиды в отношении 5:3, считая от вершины. Найдите площадь сферы, если сторона основания пирамиды равна 18 см.
----------
Проведем осевое сечение пирамиды, которое содержит осевое сечение сферы. Это равнобедренный треугольник с высотой SH, общей с высотой пирамиды.
По условию SO:ОH=5/3
Пусть коэффициент этого отношения будет х.
Тогда радиус сферы R=OH=3x.
ОК - радиус, проведенный в точку касания сферы и боковой грани пирамиды. ОК=ОН=3х.
∆ SOK- прямоугольный, c oтношением гипотенузы и катета SO:ОК=5:3 ⇒
∆ SOK- египетский, и SK=4х
Прямоугольные ∆ SOK и ∆ SHE имеют общий угол при вершине S⇒
∆ SOK~∆ SEН, из чего следует, что ∆ SHE- египетский, и
отношение SH:HE=4:3
8х:9=4:3
24х=36
х=1,5 см
R=3x=4,5 см
S sph=4πR²=81π см²
--------
Можно решать несколько иначе.
Найдём по т.Пифагора SK=4x.
KE=HE =9 ( равенство отрезков касательных из одной точки до точек касания)
Тогда SE=4x+9
SE²=SH²+HE²
(4х+9)²=(8х)²+9²
Решение уравнения даст х=1,5 см, и R=4,5, откуда Ssph=4πR²=81πсм²
----------
Проведем осевое сечение пирамиды, которое содержит осевое сечение сферы. Это равнобедренный треугольник с высотой SH, общей с высотой пирамиды.
По условию SO:ОH=5/3
Пусть коэффициент этого отношения будет х.
Тогда радиус сферы R=OH=3x.
ОК - радиус, проведенный в точку касания сферы и боковой грани пирамиды. ОК=ОН=3х.
∆ SOK- прямоугольный, c oтношением гипотенузы и катета SO:ОК=5:3 ⇒
∆ SOK- египетский, и SK=4х
Прямоугольные ∆ SOK и ∆ SHE имеют общий угол при вершине S⇒
∆ SOK~∆ SEН, из чего следует, что ∆ SHE- египетский, и
отношение SH:HE=4:3
8х:9=4:3
24х=36
х=1,5 см
R=3x=4,5 см
S sph=4πR²=81π см²
--------
Можно решать несколько иначе.
Найдём по т.Пифагора SK=4x.
KE=HE =9 ( равенство отрезков касательных из одной точки до точек касания)
Тогда SE=4x+9
SE²=SH²+HE²
(4х+9)²=(8х)²+9²
Решение уравнения даст х=1,5 см, и R=4,5, откуда Ssph=4πR²=81πсм²
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: marfingrisa4
Предмет: Химия,
автор: a9860978
Предмет: Английский язык,
автор: amangeldyaa08
Предмет: Математика,
автор: nalebedeva
Предмет: Математика,
автор: 20040705