Предмет: Алгебра,
автор: anactaciy00
постройте график функции y=x^4-25x^2+144/x^2+x-12 и определите, при каких значениях параметра K прямая y=kx+3 имеет с этим графиком не более одной общей точки. Пожалуйста помогите с рисунком.
Ответы
Автор ответа:
0
Сначала сокращаем функцию и находим те точки,которые мы обязаны выколоть:
Раскладываем числитель с заменой a=x²:

Обратная замена:
Итак,числитель имеет вид (x-4)(x+4)(x-3)(x+3).
Раскладываем знаменатель и выясняем,при каких значениях он равен нулю:

Знаменатель имеет вид (x-3)(x+4). На будущем графике мы обязаны выколоть точки при x=3 и x=-4.
Сокращаем функцию:
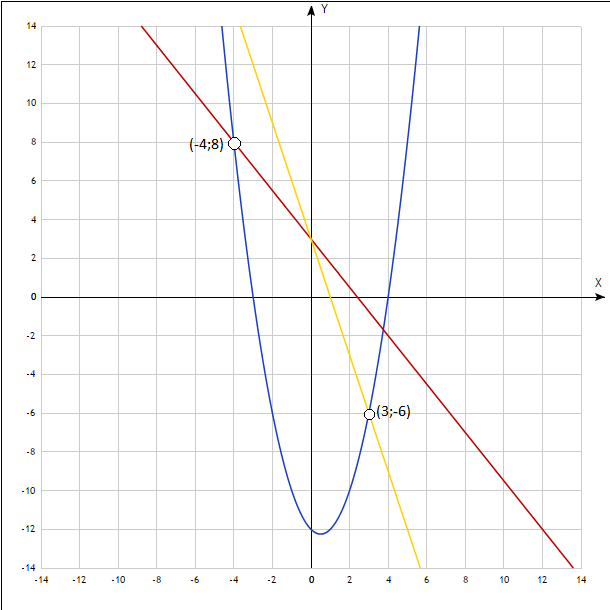
Строим график функции y=x²-x-12 с выколотыми точками (на рисунке это парабола синего цвета.Точки выколоты).
Мы обязаны знать и ординаты этих точек: При x=3 y=-6,при x=-4 y=8.
Определим функции прямых,которые будут иметь с графиком одну общую точку:
 .
.
Прямые y=-1.25x+3(на рисунке красным цветом) и y=-3x+3(жёлтым) имеют с данным графиком одну общую точку. При остальных значениях k семейство прямых y=kx+3 имеет две общие точки.
P.S.: Надеюсь,всё понятно.
Раскладываем числитель с заменой a=x²:
Обратная замена:
Итак,числитель имеет вид (x-4)(x+4)(x-3)(x+3).
Раскладываем знаменатель и выясняем,при каких значениях он равен нулю:
Знаменатель имеет вид (x-3)(x+4). На будущем графике мы обязаны выколоть точки при x=3 и x=-4.
Сокращаем функцию:
Строим график функции y=x²-x-12 с выколотыми точками (на рисунке это парабола синего цвета.Точки выколоты).
Мы обязаны знать и ординаты этих точек: При x=3 y=-6,при x=-4 y=8.
Определим функции прямых,которые будут иметь с графиком одну общую точку:
Прямые y=-1.25x+3(на рисунке красным цветом) и y=-3x+3(жёлтым) имеют с данным графиком одну общую точку. При остальных значениях k семейство прямых y=kx+3 имеет две общие точки.
P.S.: Надеюсь,всё понятно.
Приложения:
Автор ответа:
0
Да, спасибо больше
Похожие вопросы
Предмет: Обществознание,
автор: vvvvvvvvvvvvvvsss
Предмет: Українська мова,
автор: Oldgalaxygamer
Предмет: Литература,
автор: sofatarasova1111
Предмет: География,
автор: nur03
Предмет: Математика,
автор: Miamopekokc