Предмет: Алгебра,
автор: Manyusha
Ребят! Зайчики,помогите решить 73 номер
Приложения:
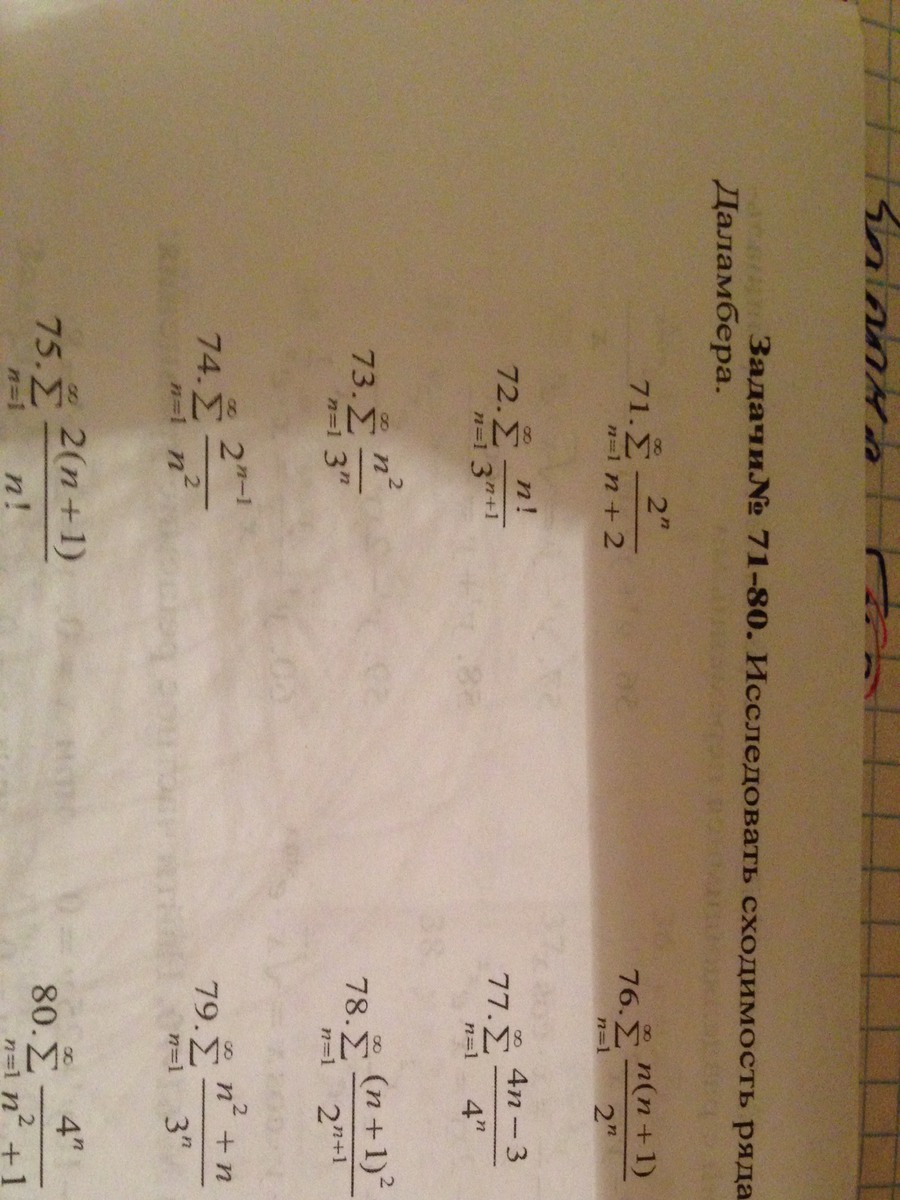
Ответы
Автор ответа:
0
Пусть  Тогда признак Даламбера гласит: если
Тогда признак Даламбера гласит: если  существует и D < 1, то ряд сходится. Докажем, что предел существует и он меньше 1:
существует и D < 1, то ряд сходится. Докажем, что предел существует и он меньше 1:  =
=  разделим числитель и знаменатель на n^2:
разделим числитель и знаменатель на n^2:  Значит по признаку Даламбера ряд сходится
Значит по признаку Даламбера ряд сходится
Похожие вопросы
Предмет: Литература,
автор: eva17594
Предмет: Математика,
автор: sofiqweex
Предмет: География,
автор: marianboiko07
Предмет: Математика,
автор: kuraevumut
Предмет: Геометрия,
автор: tanya257841157