Предмет: Математика,
автор: vladkat99
Объясните пожалуйста как тут получили ответ
Приложения:
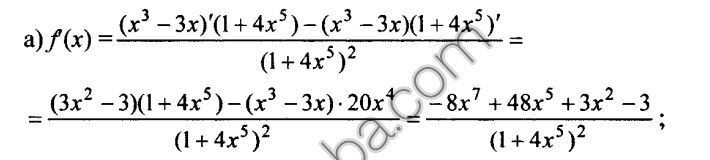
zews1065:
а в чем именно проблема, штришок за скобкой это производная, а дальше раскрыли скобки
Можете как нибудь обьяснить по подробней о раскрытие скобок
(3х*2-3)(1+4х*5)=3х*2х1+3х*2х4х*5-3х1-3х4х*5=3х*2+12х*7-3-12х*5
множится каждое число одной скобки на каждое число другой скобки
Ответы
Автор ответа:
1
1.Взяли дробь
 и нашли ее производную.
и нашли ее производную.

дальше решаем:
вначале отдельно находим производные для числителя:
(x³-3x)'=3x²-3
(1+4x^5)'=0+20x^4=20x^4
Подставляем в выражение:

дальше перемножаем скобки:

дальше решаем:
вначале отдельно находим производные для числителя:
(x³-3x)'=3x²-3
(1+4x^5)'=0+20x^4=20x^4
Подставляем в выражение:
дальше перемножаем скобки:
Похожие вопросы
Предмет: Английский язык,
автор: zanbolatagadilov
Предмет: Қазақ тiлi,
автор: zhandaulet333
Предмет: История,
автор: alibinauken
Предмет: Математика,
автор: Аноним
Предмет: Другие предметы,
автор: Diedaryxx