Question

help pls найдите точку минимума функции y=-(x^2+25600)/x

Answer 1

найдем производную,      √25600=160
y'= - (u'v-v'u)/v²=- (2x*x-x²-25600)/x²=(x²-25600)=-(x-160)(x+160)=
=(160-x)(160+x)
y'=0
в точках -160 и 160 экстремумы.
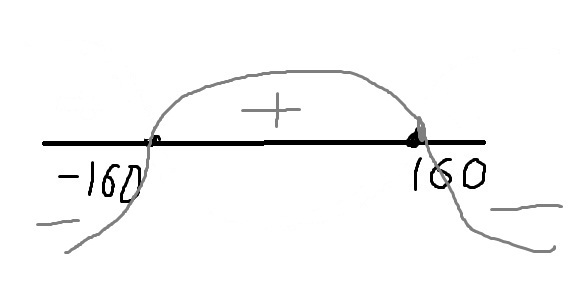
 рассмотрим знаки производной методом интервалов см рисунок 
замечаем что
в точке x=-160 производная меняет знак с - на + значит в этой точке минимум 
в качестве иллюстрации прилагается график функции