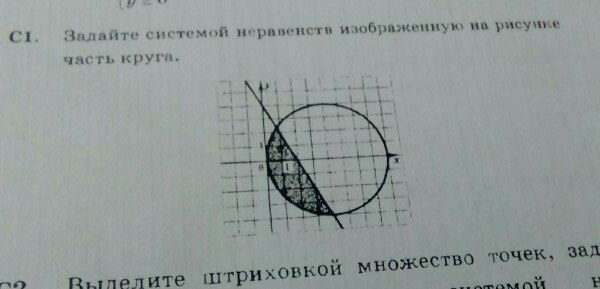
Задайте системой неравенств изображенную на рисунке часть круга
Ответы
Ответ:
Объяснение:
Круг с центром в точке O(x₀; y₀) и радиусом R описывается уравнением:
.
Каждая клетка имеет размерность 1 и поэтому центр круга находиться в точке O(4; 0) и радиус R равен 4 (см. рисунок). Тогда получим следующее уравнение для круга:
.
Так как заданная прямая не вертикальна относительно оси Ох, то уравнение прямой будем искать в виде:
Прямая проходит через точки (2; 0) и (0; 4). Подставляя эти значения получим систему уравнений и находим неизвестные k и b:
Получили следующее уравнение прямой:
По чертежу прямая должна ограничивать полуплоскость, где находиться начало координат (0; 0). Подставляем в уравнение и получим неравенство:
Тогда нужная полуплоскость, где находиться начало координат (0; 0) имеет вид:
Теперь часть круга, которая получена пересечением круга и полуплоскости, можно отобразит следующей системой неравенств:
