Question

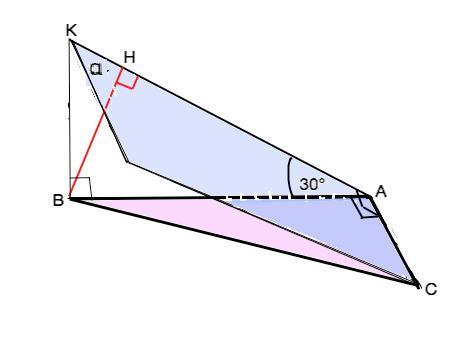
Дан треугольник ABC , угол А=90 градусов , АВ=9см . через сторону АС проведена плоскость альфа , образующияся с плоскостью треугольника АВС угол 30 градусов вычеслить расстояние от вершины в до плоскости альфа 

Answer 1

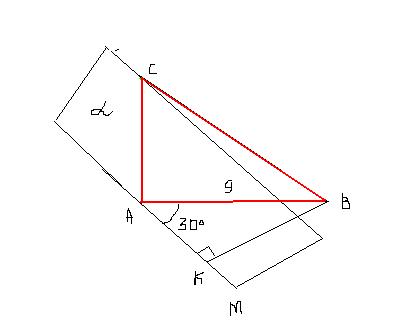
АМ - проекция плоскости альфа на плоскость перпендикулярную плоскости треугольника.

Тогда АК=sin альфа *9=4,5

Рисунок во вложении

Answer 2

Ответ: 4,5 см

Объяснение:

  Угол между плоскостями –  двугранный угол. Его величина  определяется градусной мерой линейного угла, сторонами которого являются лучи, проведённые в его гранях перпендикулярно ребру с общим началом на нём.  

 На рисунке, данном в приложении, это угол КАВ. Его стороны АК и АВ  перпендикулярны ребру АС двугранного угла: АВ как катет прямоугольного треугольника АВС, АК - как наклонная по т. о 3-х перпендикулярах.

  Расстоянием от точки  до плоскости  α является длина перпендикуляра, проведенного из  точки к данной плоскости. Отрезок ВН- перпендикуляр к плоскости α, противолежит углу НАВ, равному 30°. ВН=АВ•sin30°=9•1/2=4,5 см.