Предмет: Математика,
автор: a1998x
Помогите с решением интеграла
Приложения:
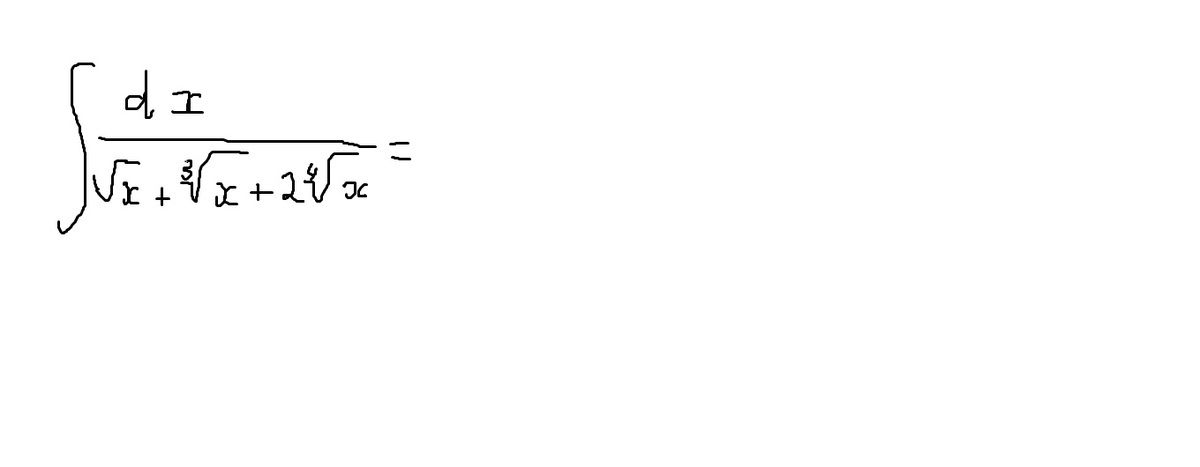
Ответы
Автор ответа:
0
Интересный интеграл, пришлось повозиться с решением.
Шаг первый -- методом неопределённых коэффициентов разбиваем дробь на простейшие
![int { frac{1}{ sqrt{x} + sqrt[3]{x}+2 sqrt[4]{x} } } , dx = int { frac{-1}{4(1+ sqrt[12]{x} )}+ frac{-1+ sqrt[12]{x} }{8(2- sqrt[12]{x}+ sqrt[6]{x} )}+ frac{1}{2 sqrt[4]{x} } - frac{1}{4 sqrt[6]{x} } } , dx
+ int { frac{1}{8 sqrt[12]{x} }} , dx int { frac{1}{ sqrt{x} + sqrt[3]{x}+2 sqrt[4]{x} } } , dx = int { frac{-1}{4(1+ sqrt[12]{x} )}+ frac{-1+ sqrt[12]{x} }{8(2- sqrt[12]{x}+ sqrt[6]{x} )}+ frac{1}{2 sqrt[4]{x} } - frac{1}{4 sqrt[6]{x} } } , dx
+ int { frac{1}{8 sqrt[12]{x} }} , dx](https://tex.z-dn.net/?f=+int+%7B+frac%7B1%7D%7B+sqrt%7Bx%7D+%2B+sqrt%5B3%5D%7Bx%7D%2B2+sqrt%5B4%5D%7Bx%7D++%7D+%7D+%2C+dx+%3D+int+%7B+frac%7B-1%7D%7B4%281%2B+sqrt%5B12%5D%7Bx%7D+%29%7D%2B+frac%7B-1%2B+sqrt%5B12%5D%7Bx%7D+%7D%7B8%282-+sqrt%5B12%5D%7Bx%7D%2B+sqrt%5B6%5D%7Bx%7D++%29%7D%2B+frac%7B1%7D%7B2++sqrt%5B4%5D%7Bx%7D+%7D+-+frac%7B1%7D%7B4+sqrt%5B6%5D%7Bx%7D+%7D++%7D+%2C+dx+%0A%0A%2B+int+%7B++frac%7B1%7D%7B8+sqrt%5B12%5D%7Bx%7D+%7D%7D+%2C+dx+)
Согласно свойству интегралу от суммы -- разбиваем на сумму интегралов и сражаемся с каждым.
![int { frac{-1}{4(1+ sqrt[12]{x}) } } , dx = -3 int { frac{ u^{11} }{(u+1)} } , du[tex]-3 int { u^{10} -u^9+u^8-u^7+u^6-u^5+u^4-u^3+u^2-u- frac{1}{u+1}+1 } , du int { frac{-1}{4(1+ sqrt[12]{x}) } } , dx = -3 int { frac{ u^{11} }{(u+1)} } , du[tex]-3 int { u^{10} -u^9+u^8-u^7+u^6-u^5+u^4-u^3+u^2-u- frac{1}{u+1}+1 } , du](https://tex.z-dn.net/?f=+int+%7B+frac%7B-1%7D%7B4%281%2B+sqrt%5B12%5D%7Bx%7D%29+%7D+%7D+%2C+dx+%3D+-3+int+%7B+frac%7B+u%5E%7B11%7D+%7D%7B%28u%2B1%29%7D+%7D+%2C+du%5Btex%5D-3+int+%7B+u%5E%7B10%7D+-u%5E9%2Bu%5E8-u%5E7%2Bu%5E6-u%5E5%2Bu%5E4-u%5E3%2Bu%5E2-u-+frac%7B1%7D%7Bu%2B1%7D%2B1+%7D+%2C+du) u =sqrt[12]{x}
[/tex]
u =sqrt[12]{x}
[/tex]
Простейшие первообразные, сразу заменяем u на x (обратно), в дальнейшем я такие тривиальные шаги буду опускать:
![= frac{3 sqrt[12]{x^{11}} }{11} + frac{3x^{5/6}}{10} - frac{x^{3/4}}{3} + frac{3x^{2/3}}{8} - frac{3x^{7/12}}{7} - frac{3x^{5/12}}{5} + frac{ sqrt{x} }{2} + frac{3 sqrt[3]{x} }{4} - sqrt[4]{x}+
+(3 sqrt[6]{x} )/2 - 3 sqrt[12]{x} + 3ln( sqrt[12]{x} +1) + const = frac{3 sqrt[12]{x^{11}} }{11} + frac{3x^{5/6}}{10} - frac{x^{3/4}}{3} + frac{3x^{2/3}}{8} - frac{3x^{7/12}}{7} - frac{3x^{5/12}}{5} + frac{ sqrt{x} }{2} + frac{3 sqrt[3]{x} }{4} - sqrt[4]{x}+
+(3 sqrt[6]{x} )/2 - 3 sqrt[12]{x} + 3ln( sqrt[12]{x} +1) + const](https://tex.z-dn.net/?f=%3D+frac%7B3+sqrt%5B12%5D%7Bx%5E%7B11%7D%7D+%7D%7B11%7D+%2B+frac%7B3x%5E%7B5%2F6%7D%7D%7B10%7D+-+frac%7Bx%5E%7B3%2F4%7D%7D%7B3%7D+%2B+frac%7B3x%5E%7B2%2F3%7D%7D%7B8%7D+-+frac%7B3x%5E%7B7%2F12%7D%7D%7B7%7D+-+frac%7B3x%5E%7B5%2F12%7D%7D%7B5%7D+%2B+frac%7B+sqrt%7Bx%7D+%7D%7B2%7D+%2B+frac%7B3+sqrt%5B3%5D%7Bx%7D+%7D%7B4%7D+-+sqrt%5B4%5D%7Bx%7D%2B%0A%0A%2B%283+sqrt%5B6%5D%7Bx%7D+%29%2F2+-+3+sqrt%5B12%5D%7Bx%7D+%2B+3ln%28+sqrt%5B12%5D%7Bx%7D+%2B1%29+%2B+const)
![int { frac{-1+ sqrt[12]{x} }{8(2- sqrt[12]{x}+ sqrt[6]{x} )} } , dx = frac{3 sqrt[12]{x^{11}} }{22} - frac{x^{3/4}}{3} - frac{3x^{2/3}}{8} + frac{3x^{7/12}}{7} + frac{3x^{5/12}}{5} + frac{3 sqrt{x} }{2}+
+ (15 sqrt[3]{x} )/4 -7 sqrt[4]{x} +(9x^{1/6})/2+51 sqrt[12]{x} +(33ln( sqrt[6]{x}- sqrt[12]{x}+2 ))/2-
-(171arctg[(2 sqrt[12]{x}-1 )/( sqrt[7]{x}) ])/ sqrt[7]{x} +const int { frac{-1+ sqrt[12]{x} }{8(2- sqrt[12]{x}+ sqrt[6]{x} )} } , dx = frac{3 sqrt[12]{x^{11}} }{22} - frac{x^{3/4}}{3} - frac{3x^{2/3}}{8} + frac{3x^{7/12}}{7} + frac{3x^{5/12}}{5} + frac{3 sqrt{x} }{2}+
+ (15 sqrt[3]{x} )/4 -7 sqrt[4]{x} +(9x^{1/6})/2+51 sqrt[12]{x} +(33ln( sqrt[6]{x}- sqrt[12]{x}+2 ))/2-
-(171arctg[(2 sqrt[12]{x}-1 )/( sqrt[7]{x}) ])/ sqrt[7]{x} +const](https://tex.z-dn.net/?f=+int+%7B+frac%7B-1%2B+sqrt%5B12%5D%7Bx%7D+%7D%7B8%282-+sqrt%5B12%5D%7Bx%7D%2B+sqrt%5B6%5D%7Bx%7D++%29%7D+%7D+%2C+dx+%3D+frac%7B3+sqrt%5B12%5D%7Bx%5E%7B11%7D%7D+%7D%7B22%7D+-+frac%7Bx%5E%7B3%2F4%7D%7D%7B3%7D+-+frac%7B3x%5E%7B2%2F3%7D%7D%7B8%7D+%2B+frac%7B3x%5E%7B7%2F12%7D%7D%7B7%7D+%2B+frac%7B3x%5E%7B5%2F12%7D%7D%7B5%7D+%2B+frac%7B3+sqrt%7Bx%7D+%7D%7B2%7D%2B%0A%0A%2B+%2815+sqrt%5B3%5D%7Bx%7D+%29%2F4+-7+sqrt%5B4%5D%7Bx%7D+%2B%289x%5E%7B1%2F6%7D%29%2F2%2B51+sqrt%5B12%5D%7Bx%7D+%2B%2833ln%28+sqrt%5B6%5D%7Bx%7D-+sqrt%5B12%5D%7Bx%7D%2B2++%29%29%2F2-%0A%0A-%28171arctg%5B%282+sqrt%5B12%5D%7Bx%7D-1+%29%2F%28+sqrt%5B7%5D%7Bx%7D%29+%5D%29%2F+sqrt%5B7%5D%7Bx%7D+%2Bconst)
Будьте внимательны, красивыми формулами сайта писать уже затруднительно, но логика сохранена, всё записано истинно
Три последних интеграла берутся без затруднений, данный момент опущу.
Дальше арифметика, просуммировав все результаты, и набросив косметики, ответ представляет собой:
![2 sqrt{x} -3 sqrt[3]{x} -8 sqrt[4]{x} +6 sqrt[6]{x} +48 sqrt[12]{x} +3ln( sqrt[12]{x}+1 )
+ (33/2) ln( sqrt[6]{x}- sqrt[12]{x}+2) - (171/ sqrt[7]{x} )arctg[(2x^{1/12}-1)/(x^{1/7})] +
+ const 2 sqrt{x} -3 sqrt[3]{x} -8 sqrt[4]{x} +6 sqrt[6]{x} +48 sqrt[12]{x} +3ln( sqrt[12]{x}+1 )
+ (33/2) ln( sqrt[6]{x}- sqrt[12]{x}+2) - (171/ sqrt[7]{x} )arctg[(2x^{1/12}-1)/(x^{1/7})] +
+ const](https://tex.z-dn.net/?f=2+sqrt%7Bx%7D+-3+sqrt%5B3%5D%7Bx%7D+-8+sqrt%5B4%5D%7Bx%7D+%2B6+sqrt%5B6%5D%7Bx%7D+%2B48+sqrt%5B12%5D%7Bx%7D+%2B3ln%28+sqrt%5B12%5D%7Bx%7D%2B1+%29%0A%0A%2B+%2833%2F2%29+ln%28+sqrt%5B6%5D%7Bx%7D-+sqrt%5B12%5D%7Bx%7D%2B2%29+-+%28171%2F+sqrt%5B7%5D%7Bx%7D+%29arctg%5B%282x%5E%7B1%2F12%7D-1%29%2F%28x%5E%7B1%2F7%7D%29%5D+%2B%0A%0A%2B+const)
Шаг первый -- методом неопределённых коэффициентов разбиваем дробь на простейшие
Согласно свойству интегралу от суммы -- разбиваем на сумму интегралов и сражаемся с каждым.
Простейшие первообразные, сразу заменяем u на x (обратно), в дальнейшем я такие тривиальные шаги буду опускать:
Будьте внимательны, красивыми формулами сайта писать уже затруднительно, но логика сохранена, всё записано истинно
Три последних интеграла берутся без затруднений, данный момент опущу.
Дальше арифметика, просуммировав все результаты, и набросив косметики, ответ представляет собой:
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Алгебра,
автор: vikavikavikabi
Предмет: Қазақ тiлi,
автор: Аноним
Предмет: Математика,
автор: tankak