Question

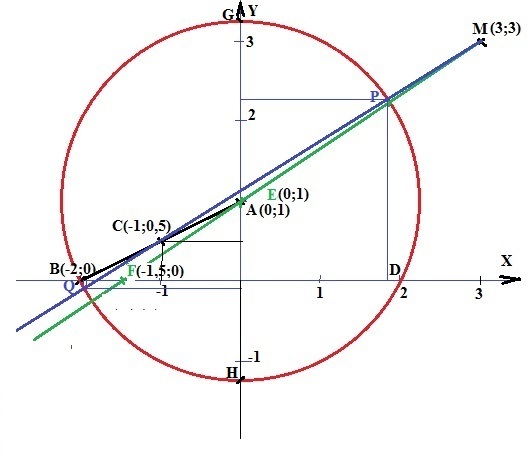
  Зачетная работа по геометрии 8 класс по теме: "Декартовы координаты на плоскости".

 

 

А (0;1)

В (-2;0)

М (3;3)

 

 

 

 

 

 

 

 

 

 

 

 

 

Answer 1

1. Координаты вектора равны разности соответствующих координат точек его конца и начала. Модуль вектора (его длина) равен квадратному корню из суммы квадратов его координат.

|AB|=√((-2)²+((-1)²) = √5 ед.

2. Координаты середины отрезка находятся как среднее арифметическое соответсятвующих координат начала и конца этого отрезка.

Xc=(Xa+Xb)/2 = (0-2)/2 = -1.

Yc=(Ya+Yb)/2 = (1+0)/2 = 0,5.

C(-1;0,5)

3. Уравнение окружности: (X-Xц)²+(Y-Yц)²=R².

В нашем случае: центр А(0;1), R=|AB|=√5. Уравнение окружности:

X²+(Y-1)²=5.

4. Чтобы найти координаты точек пересечения данной окружности с осями координат, надо в уравнение окружности подставить значения

Y=0 и X=0 и решить получившееся уравнение:

X²+(0-1)²=5. => X1=2, X2= -2.

0 +(Y²-2Y+1)=5 => Y1=1+√5≈ 3,24, Y2=1-√5≈ -1,24.

Точки пересечения:

с осью Х: D(2;0) и B(-2;0).

с осью Y: G(0;3,24) и H(0;-1,24)

5. Уравнение прямой АМ:

Каноническое: (X-Xa)/(Xm-Xa)=(Y-Ya)/(Ym-Ya) или

X/3=(Y-1)/2 => общее уравнение: 2X-3Y+3=0 =>

уравнение с угловым коэффициентом: y=(2/3)*X+1.

6. Точки пересечения E и F с осями координат (по п.4):

3Y=3 => Ye=1. 2X+3=0 => Xf=-3/2 = -1,5.

Точки пересечения прямой АМ с осями координат:

E(0;1) и F(-1,5;0).

7. Модуль вектора MC (его длина):

|MC|= √(Xc-Xm)²+(Yc-Ym)²) = √(-1-3)²+(0,5-3)²) =√(16+6,25).

|MC|≈ 4,72 ед.

8. Уравнение прямой МС:

(X-Xm)/(Xc-Xm)=(Y-Ym)/(Yc-Ym) => (X-3)/(-4)=(Y-3)/-2,5) =>

2,5X-4Y+4,5=0 => 5X-8Y+9=0.

Точки пересечения прямой МС и окружности X²+(Y-1)²=5 найдем,

решив систему уравнений:

X²+Y²-2Y=4 (1) и 5X-8Y+9=0 (2).

Y=(5/8)X+(9/8). Подставим это значение в (1):

X²+((5/8)X+9/8)²-(10/8)X-18/8 = 4 или

(64/64)X²+(25/64)X²+(90/64)X+81/64-(80/64)X-144/64=256/64 =>

89X²+10X-319=0 =>

X1=(-5+√(25+28391)/89 ≈ 1,8. => Y1≈2,25.

X2=(-5-√(25+28391)/89 ≈-1,9. => Y1≈-0,1.

Искомые точки:

P(1,8;2,25) и Q(-1,9;-0,1)