Предмет: Математика,
автор: galyaneizhko
Найдите точку максимума функции 11+ 6х- х^3/3.
Ответы
Автор ответа:
0
РЕШЕНИЕ
Для этого надо найти точку, где производная равна 0.
Y = - 1/3*x³ + 6x + 11
Y' = x² - 6 = 0
Корни уравнения - точки экстремума = +// √6 (~2.45)
Ymin= Y(-√6) = ~ 1.202 - ОТВЕТ
Ymax = Y(+√6) = ~ 20.798 - ОТВЕТ
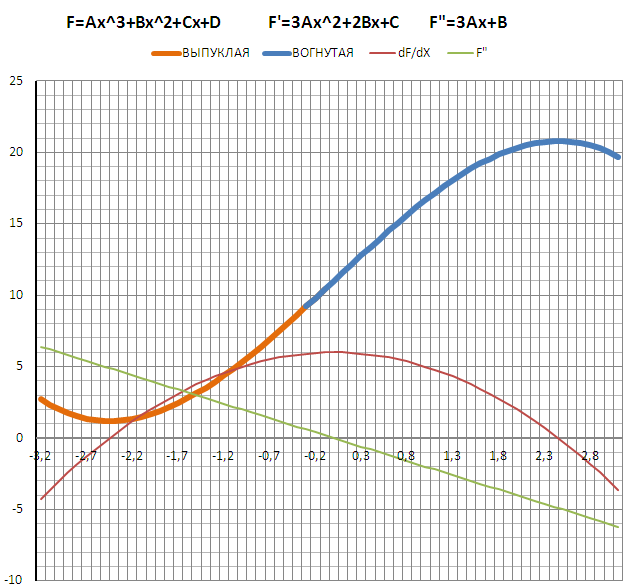
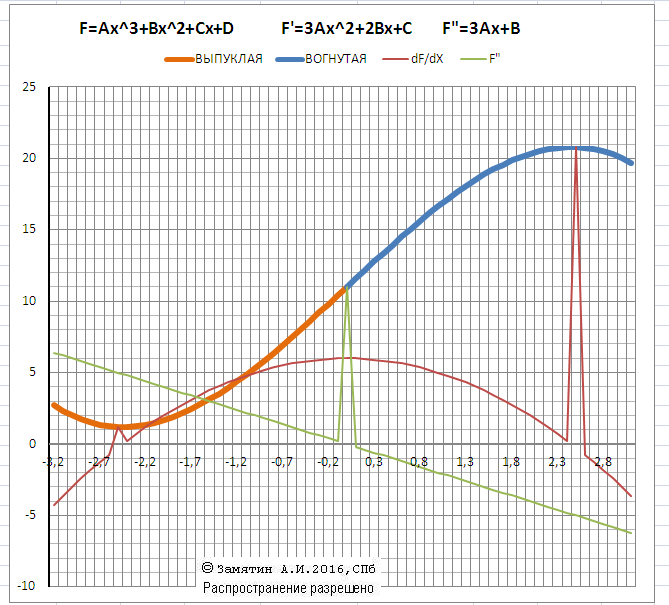
Дополнительно - расчет подтвержден графиками функции и двух её производных.
Для этого надо найти точку, где производная равна 0.
Y = - 1/3*x³ + 6x + 11
Y' = x² - 6 = 0
Корни уравнения - точки экстремума = +// √6 (~2.45)
Ymin= Y(-√6) = ~ 1.202 - ОТВЕТ
Ymax = Y(+√6) = ~ 20.798 - ОТВЕТ
Дополнительно - расчет подтвержден графиками функции и двух её производных.
Приложения:
Автор ответа:
0
ответ должен быть 4, корень из 6 я не смогу в бланк ЕГЭ записать!
Автор ответа:
0
ГРАФИК и решение - точное. Где-то ошибка
Автор ответа:
0
Производная ТОЧНО 6-х^2=0 - проверено
Автор ответа:
0
В БЛАНК - можно записать ВСЁ.- было бы правильно
Похожие вопросы
Предмет: Химия,
автор: arab333
Предмет: Математика,
автор: joni200812
Предмет: Литература,
автор: pollyberdigulovababy
Предмет: Химия,
автор: маяда