Предмет: Алгебра,
автор: Romanova3
Помогите с решением, пожалуйста
Приложения:
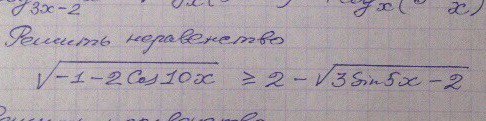
Ответы
Автор ответа:
0
√(-1-2cos10x) ≥ 2 -√(3sin5x -2) ;
√(4sin²5x -3) ≥ 2 -√(3sin5x -2) ;
√(4sin²5x -3) + √(3sin5x -2) ≥ 2 ;
ОДЗ: sin5x≥(√3)2 .
* * * {4sin²5x -3≥0 ; 3sin5x -2≥0. ⇔
{4(sin5x +√3/2)(sin5x -√3/2) ≥0 ; sin5x≥2/3. ⇒ sin5x≥(√3)2 * * *
max(√(4sin²5x -3) + √(3sin5x -2) ) =2 , если sin5x =1.
(только равно, невозможно > 2 )
5x =π/2+2πn , n∈Z ⇔x =π/10+2πn/5 , n∈Z.
ответ: π/10+2πn/5 , n∈Z.
√(4sin²5x -3) ≥ 2 -√(3sin5x -2) ;
√(4sin²5x -3) + √(3sin5x -2) ≥ 2 ;
ОДЗ: sin5x≥(√3)2 .
* * * {4sin²5x -3≥0 ; 3sin5x -2≥0. ⇔
{4(sin5x +√3/2)(sin5x -√3/2) ≥0 ; sin5x≥2/3. ⇒ sin5x≥(√3)2 * * *
max(√(4sin²5x -3) + √(3sin5x -2) ) =2 , если sin5x =1.
(только равно, невозможно > 2 )
5x =π/2+2πn , n∈Z ⇔x =π/10+2πn/5 , n∈Z.
ответ: π/10+2πn/5 , n∈Z.
Похожие вопросы
Предмет: Алгебра,
автор: leralera52
Предмет: Математика,
автор: denisthcbk
Предмет: Английский язык,
автор: jkkkkkkk42
Предмет: Математика,
автор: davydovajulika