Предмет: Математика,
автор: Physic79832
Помогите решеить 30.41 г (не понимаю как одз под корнем разложить)!!!
Приложения:
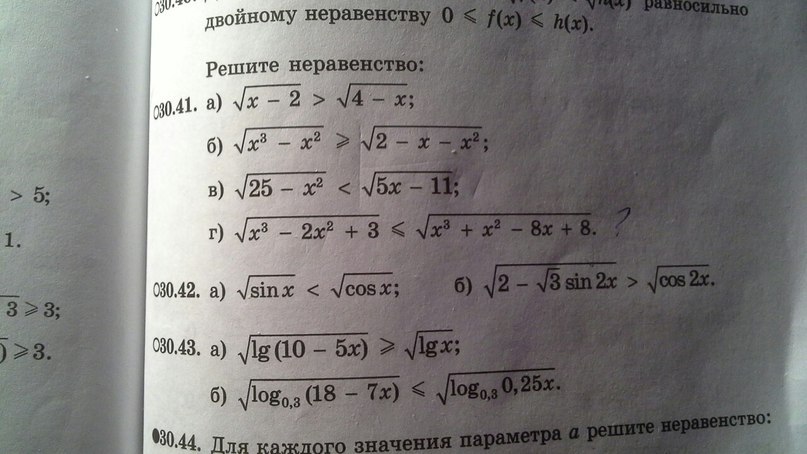
Ответы
Автор ответа:
0
до -2 производная положительна, значит функция растет. от -2 до 4/3 убывает, и от 4/3 опять растет. В точке 4/3 (проверяется) функция принимает положительное значение. Значит у функции единственный корень, меньший -2. Поэтому из области определения первого подкоренного выражения x>=-1, второе подкоренное всегда положительно.
Теперь возводим все в квадрат и получаем
Вместе с областью определения имеем:
x∈[-1,1]∪[5/3,+∞)
Автор ответа:
0
Огромное спасибо
Автор ответа:
0
мог бы каждый так адекватно объяснять
Автор ответа:
0
а при проверке функции надо xmin в исходное уравнение подставлять или в производную?
Автор ответа:
0
4/3 в исходную подкоренную надо подставлять, чтоб убедиться, что подкоренное выражение больше 0
Похожие вопросы
Предмет: Информатика,
автор: Аноним
Предмет: Математика,
автор: madina54148
Предмет: Математика,
автор: fanskeleton1
Предмет: Математика,
автор: ramzeslina
Предмет: Математика,
автор: htgf