Середины сторон некоторого четырехугольника являются вершинами другого четырехугольника. Найдите петиметр второго четырехугольника, если диагонали первого четырехугольника равны 18 и 32.
Ответы
пусть первый четырехугольник: АВСД, середины сторон соответственно:
а - АВ, в - ВС, с - СД, д - ДА,
т.е. Аа=аВ, Вв=вС, Сс=сД, Дд=дА
известны длины диагоналей АС = 18 и ВД=32, надо найти периметр четырехугольника авсд.
1) нарисуй чертеж - и посмотри на треугольники АВС и аВв.
у них:
- углы АВС и аВв равны (это один и тот же угол - В),
- стороны АВ и ВС пропорциональны аВ и Вв (аВ=1/2 АВ, а вВ=1/2ВС),
значит, треугольники подобны и, соответственно, ав = 1/2 АС = 9,
а также равны углы Вав=ВАС, Вва=ВСА - следовательно стороны ав и АС - параллельны.
2) аналогично расссмотрим треугольники АДС и дДс - они тоже подобны,
и, соответственно, стороны дс и АС параллельны и да=1/2 АС,
и, вспомнив 1) - находим, что ав параллельно дс и ав=дс=1/2 АС
3) аналогично рассмотрим треугольники ВСД и вСд - аналогично докажем, что они тоже подобны и найдем, что ВД параллельно вд и вд=1/2 ВД,
а также подобны треугольники ВАД и аАс, и соответственно, получим, что ВД параллельно ас и ас=1/2ВД
следовательно ас параллельно вд и ас=вд=1/2 ВД=16
4) т.е. мы увидели, что малый четырехугольник у нас - параллелограмм (это, в принципе, не важно, но красиво), но главное - мы знаем все его стороны: 9,16,9,16, соответственно, периметр равен
ав+вс+сд+ад=50
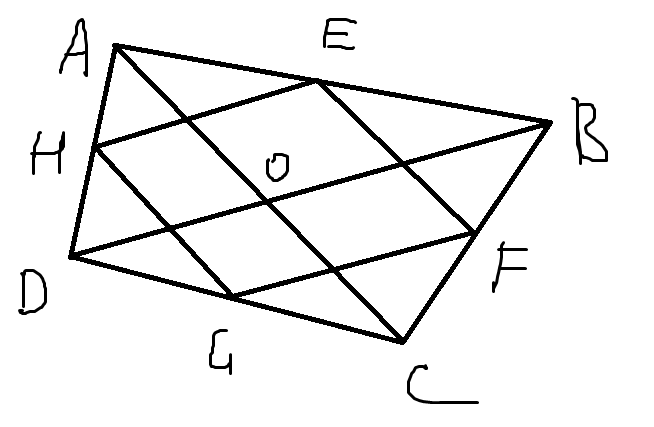
рассмотрим треугольник АВС: EF - средняя линия ⇒ EF = 1/2 AC
рассмотрим треугольник АDC: HG - средняя линия ⇒ HG = 1/2 AC
рассмотрим треугольник DCB: FG - средняя линия ⇒FG = 1/2 DB
рассмотрим треугольник DAB: HE - средняя линия ⇒ HE = 1/2 DB
1/2 AC + 1/2 AC + 1/2 DB + 1/2 DB = AC + BD = 18+32=50
ответ: 50