Question

помогите, буду очень благодарна!

Радиус окружности, вписанной в круговой сектор, в 3 раза меньше радиуса сектора. Найдите длину окружности, вписанной в сектор, если площадь сектора равна 24*пи см квадратных

Answer 1

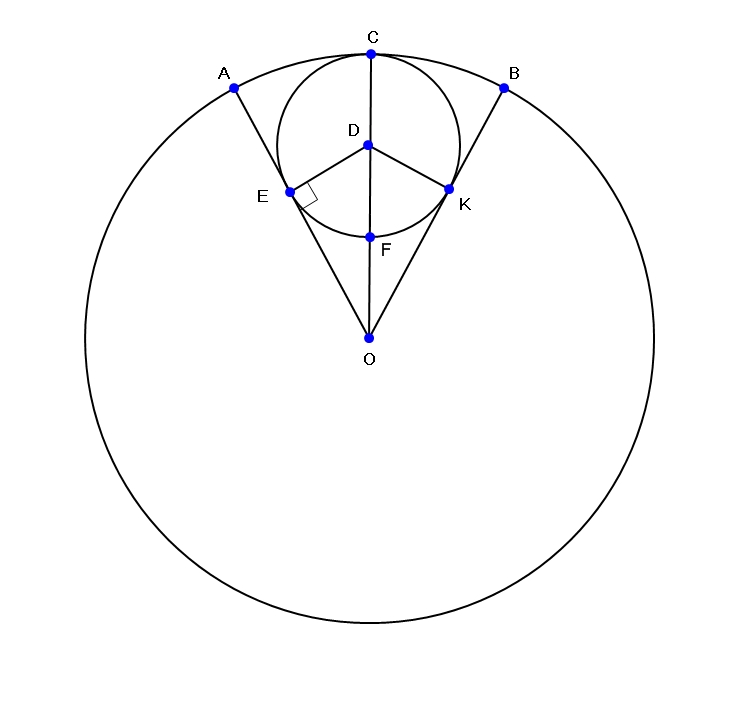
См. рисунок во вложении

АОВ- центральный угол сегмента

Площадь сегмента S=пи*R^2*(угол AOB)/360, где R -радиус основной окружности.

Обозначим r - радиус вписанной окружности

DE - перпендикуляр из центра вписанной окружности на радиус AO.

CD=DF=DE=r

R=3*r

CO=R, CD+DF=2*r, значит, FO=r

DF+FO = 2*r

В треугольнике OED sin угла(EOD)=DE/DO=1/2

Угол EOD=30 градусов, он равен половине центрального угла сегмента (это очевидно из рассмотрения треугольников EDO и DOK), значит, центральный угол равен 60 градусов

S=пи*R^2*60/360=24*пи, откуда R^2=144, R=12

r=R/3=4

Длина  вписанной окружности hfdyf  2*пи*r=8*пи