Предмет: Математика,
автор: dino8zavr
Дан квадрат, одна сторона которого разделена пополам и соединена вершиной-отрезком, ограничивающим заштрихованный треугольник.
Также даны 2 ящика: в первом - 3 белых и 2 черных шара, а во втором - 2 белых и 4 черных шара.
В квадрате наугад выбирается точка. Если она попала в заштрихованную область, то выбирается шар из первого ящика, в противном случае из второго.
а) найти вероятность того, что шар оказался черным
б) пусть извлеченный шар оказался черным. найти вероятность того, что точка попала в заштрихованный треугольник.
Ответы
Автор ответа:
2
РЕШЕНИЕ
Два события - попасть ы заштрихованную часть И выбрать черный.
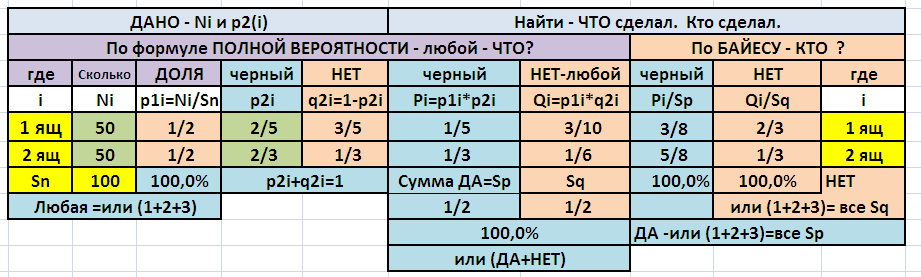
Расчет приведен в приложении.
Событие 1 - попасть в заштрихованную часть - 50/50 - вероятность р1=0,5
Вероятности черного шара в ящиках - р2(1) = 2/5 и р2(2) = 4/6=2/3
Далее - вероятность двух событий И первый И черный ИЛИ И второй И черный
Р1 = 1/2 * 2/5 +1/2*1/3 = 1/2 + 1/3 = 1/2 - вероятность черного
И теперь по формуле Байеса
Для первого ящика 1/5 : 1/2 = 3/8
для второго ящика 1/3 : 1/2 = 5/8 = 0,625 = 62,5% - ОТВЕТ
Два события - попасть ы заштрихованную часть И выбрать черный.
Расчет приведен в приложении.
Событие 1 - попасть в заштрихованную часть - 50/50 - вероятность р1=0,5
Вероятности черного шара в ящиках - р2(1) = 2/5 и р2(2) = 4/6=2/3
Далее - вероятность двух событий И первый И черный ИЛИ И второй И черный
Р1 = 1/2 * 2/5 +1/2*1/3 = 1/2 + 1/3 = 1/2 - вероятность черного
И теперь по формуле Байеса
Для первого ящика 1/5 : 1/2 = 3/8
для второго ящика 1/3 : 1/2 = 5/8 = 0,625 = 62,5% - ОТВЕТ
Приложения:
dino8zavr:
простите, а что за приложение?
Похожие вопросы
Предмет: Информатика,
автор: depp81
Предмет: История,
автор: Аноним
Предмет: Русский язык,
автор: sabitinkar0
Предмет: Українська мова,
автор: tatianak7
Предмет: Математика,
автор: SeRiLis