в основі піраміди лежить прямокутник,одна із сторін якої дорівнює 8 см,всі бічні ребра піраміди по 13 см.Обчисліть обєм піраміди,якщо її висота дорівнює 12см.
Ответы
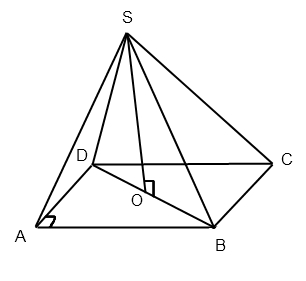
Для удобства перепишу ваше условие в соответствии с рисунком:
BC = 8 см, SO = 12 см, SC = SD = SA = SB = 13 см.
Вершина S проектируется в центр описанной окружности O, так как боковые ребра равны.
В прямоугольном треугольнике SOB: OB - половина диагонали прямоугольника ABCD.
По теореме Пифагора: OB ² = SB ² - SO ²
OB ² = 13 ² - 12 ² = 169 - 144 = 25
OB = 5 см.
Значит диагональ ABCD равна 2OB = 10 см.
В прямоугольном треугольнике ABD: AD = 8 см, DB = 10 см.
По теореме Пифагора: AB ² = DB ² - AD ²
AB ² = 10 ² - 8 ² = 100 - 64 = 36.
AB = 6 см.
Объем пирамиды вычисляется по следующей формуле:
V = 1/3 * S * h, где S - площадь основания, h - высота пирамиды.
S = AD * AB = 8 * 6 = 48 см ².
V = 1/3 * 48 * 12 = 48 * 4 = 192 см ³.