Предмет: Алгебра,
автор: Озг
Доказать тождество (2а/а+3-4а/а^2+6а+9)а+1/а^2-9-а^2-9а/а+3=а
Приложения:
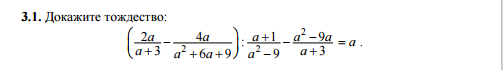
Ответы
Автор ответа:
53
Доказать тождество
[2а/(а+3)-4а/(а^2+6а+9)] :[(а+1)/(а^2-9)] - (а^2-9а)/(а+3)=а
[2а/(а+3)-4а/(а^2+6а+9)] :[(а+1)/(а^2-9)] - (а^2-9а)/(а+3)
1) [2а/(а+3)-4а/(а^2+6а+9)]=[(2а(а+3)-4а)/((а+3)^2)]=2a(a+1)/((а+3)^2
2) (а+1)/(а^2-9)=(а+1)/[(а-3)(a+3)]
3) [2a(a+1)/((а+3)^2] :[(а+1)/(а^2-9)]=
=[2a(a+1)/((а+3)^2] · [(а-3)(a+3)]/(а+1)=2a(a-3)/(a+3)
4)2a(a-3)/(a+3)- (а^2-9а)/(а+3)=[2a^2-6a-a^2+9a]/(a+3)=(a^2+3a)/(a+3)=a(a+3)/(a+3)=a
[2а/(а+3)-4а/(а^2+6а+9)] :[(а+1)/(а^2-9)] - (а^2-9а)/(а+3)=а
[2а/(а+3)-4а/(а^2+6а+9)] :[(а+1)/(а^2-9)] - (а^2-9а)/(а+3)
1) [2а/(а+3)-4а/(а^2+6а+9)]=[(2а(а+3)-4а)/((а+3)^2)]=2a(a+1)/((а+3)^2
2) (а+1)/(а^2-9)=(а+1)/[(а-3)(a+3)]
3) [2a(a+1)/((а+3)^2] :[(а+1)/(а^2-9)]=
=[2a(a+1)/((а+3)^2] · [(а-3)(a+3)]/(а+1)=2a(a-3)/(a+3)
4)2a(a-3)/(a+3)- (а^2-9а)/(а+3)=[2a^2-6a-a^2+9a]/(a+3)=(a^2+3a)/(a+3)=a(a+3)/(a+3)=a
Похожие вопросы
Предмет: ОБЖ,
автор: farmf0713
Предмет: Английский язык,
автор: dariairiska30
Предмет: Математика,
автор: alya210113
Предмет: Математика,
автор: avto5574
Предмет: История,
автор: savva228pri