Предмет: Геометрия,
автор: 15lD
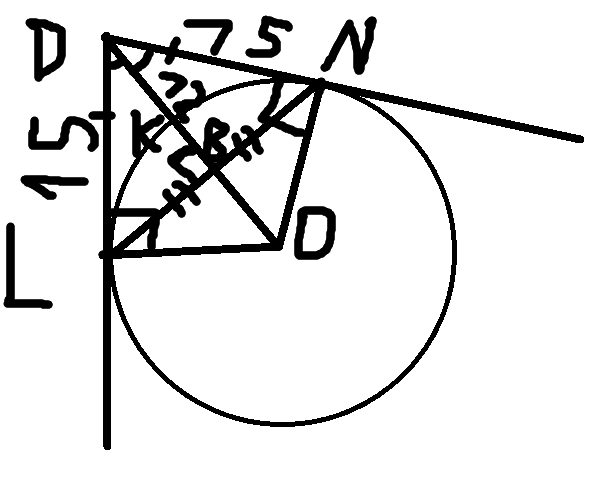
Помогите... К окружности с центром О проведены касательные DN и DL ( N и L -точки касания). Отрезки DO и NL пересекаются в точке В. Найдите длину отрезка NL, если DN=15. BD=12.
Ответы
Автор ответа:
21
Т.к. касательные DN и DL проведены из одной точки D, то они равны: DN=DL=15=> треугольник LDN-равнобедренный, значит если DO-биссектриса (по свойству отрезка из общей точки касательных к центру окружности), то DO-еще и медиана и высота; По теореме Пифагора BN= см=
см= см=9см. Т.к. DB - медиана, то NL=2BN=2*9см=18см.
см=9см. Т.к. DB - медиана, то NL=2BN=2*9см=18см.
Ответ: NL=18 см.
Ответ: NL=18 см.
Приложения:
Похожие вопросы
Предмет: Математика,
автор: fjfghfgh46
Предмет: Биология,
автор: scbgdg32
Предмет: Химия,
автор: mariarabokon11
Предмет: Английский язык,
автор: ОтвечуВсем
Предмет: Математика,
автор: ermolova0908