Предмет: Геометрия,
автор: yaoi1
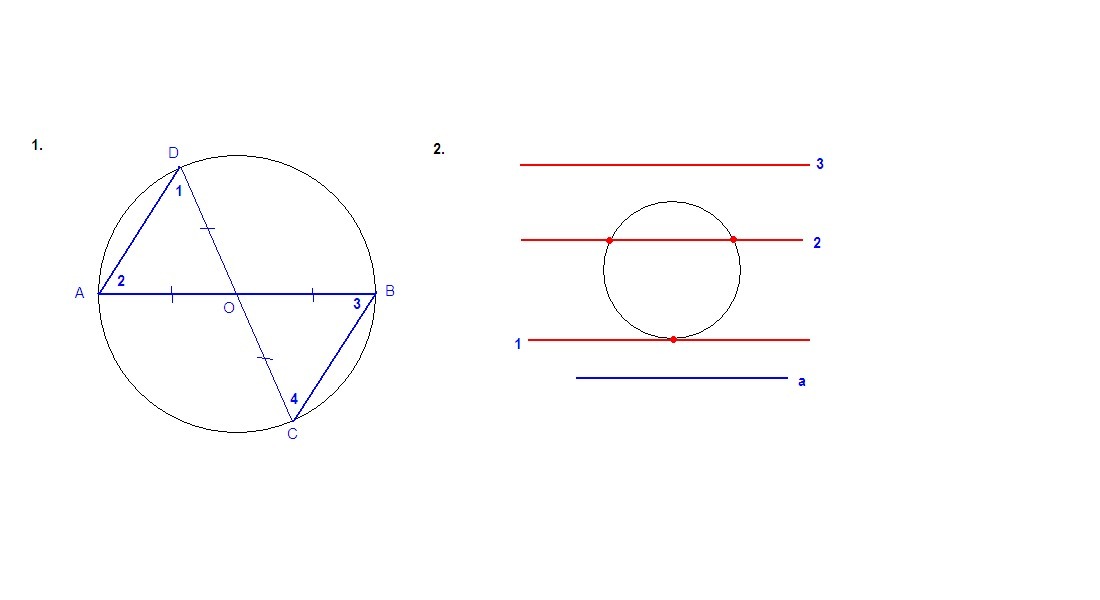
1)через концы диаметра AB окружности с центром O проведены параллельные хорды BC и AD . Докажите , что AD=BC
2) на данной окружности постройте точку , находящуюся на данном расстоянии от данной прямой . Сколько решений может иметь задача ?
Ответы
Автор ответа:
117
1. Соединим точки С и D с центром. Тогда треугольники AOD и ВОС равнобедренные (OA = OB = OC = OD как радиусы), ⇒
∠1 = ∠2 и ∠3 = ∠4.
∠2 = ∠3 как накрест лежащие при пересечении параллельных прямых AD и ВС секущей АВ. Но тогда в этих треугольниках равны и углы при вершине О. Значит треугольники AOD и ВОС равны по двум сторонам и углу между ними, ⇒
AD = BC.
2. Точки, находящиеся на данном расстоянии от данной прямой а, будут расположены на прямой, параллельной прямой а (красные прямые). В зависимости от расположения прямых задача может иметь одно решение (1), два решения (2) и не иметь решения (3).
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: gohatop41
Предмет: География,
автор: mobile232009
Предмет: Алгебра,
автор: pasivka20
Предмет: История,
автор: katyaivanova85
Предмет: История,
автор: katyaivanova85