Question

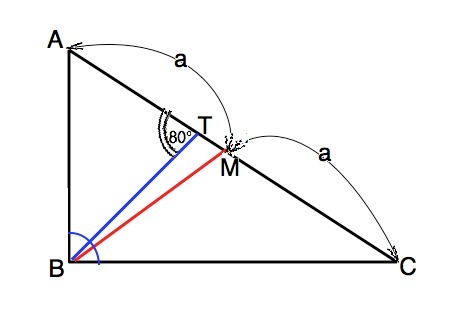
Найдите угол С треугольника АВС,если его медиана ВМ равна половине стороны АС,а угол ВТА,образованный биссектрисой ВТ и стороной АС,равен 80 градусов

Answer 1

В треугольнике АВС медиана ВМ равна половине стороны АС (дано), следовательно, треугольник АВС - прямоугольный (<B = 90° по свойству медианы прямоугольного треугольника). Биссектриса ВТ  прямого угла делит его на углы АВТ и ТВС, равные 45°. Угол АТВ равен 80° (дано). Это внешний угол треугольника ВТС и равен сумме двух внутренних углов, не смежных с ним, то есть <TBC+<BCT = <ATB или <BCT = 80° - 45° = 35°.

Ответ: <C = 35°.

Answer 2

 По условию ВМ=АМ=СМ, т.е. ВМ=АС:2.   Если медиана треугольника равна половине стороны, к которой она проведена, то угол напротив этой стороны равен 90º. Следовательно, угол АВС=90°, и углы, на которые биссектриса ВТ делит его, равны 45°. Из суммы углов треугольника в ∆ АВТ угол А=180°-∠АТВ-∠АВТ=180°-80°-45°=55°. Из суммы углов треугольника АВС угол С=180°-90°-55°=35°