Предмет: Алгебра,
автор: Липа9
помогите....................
Приложения:
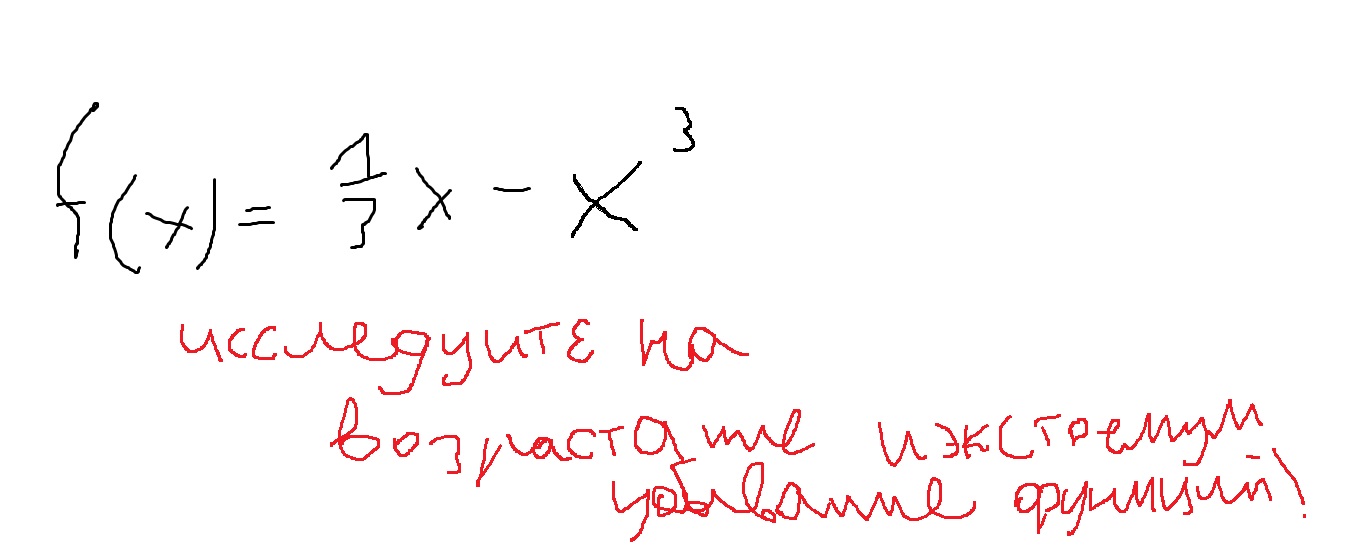
Ответы
Автор ответа:
0
(-∞; -1/3)v(1/3;∞)убыв
(-1/3; 1/3)возр
х=-1/3 min
x=1/3 max
Автор ответа:
0
Найдем производную данной функции:
f`(x)=1/3-3x^2
Найдем точки экстремума,приравнивая к нулю:
1/3-3x^2=0
x1=1/3
x2=-1/3
-Чертим числовую прямую,и отмечаем на ней данные точки.
-Выделяем промежутки на данной прямой и получаем,что
(-бесконечность;(-1/3)) и (1/3;+бесконечность)----функция убывает
((-1/3);1/3)----функция возраставет.
Значит 1/3-точка максимума,а -(1/3)-точка минимума.
Похожие вопросы
Предмет: Русский язык,
автор: nuralmedjidov
Предмет: География,
автор: Аноним
Предмет: Математика,
автор: davisonfrenk
Предмет: Математика,
автор: 1010100