Предмет: Алгебра,
автор: luckyguy
∫dx/(x^2+9)^3
рациональная дробь 4 вида.
Ответы
Автор ответа:
0
решение в файле............................
Приложения:
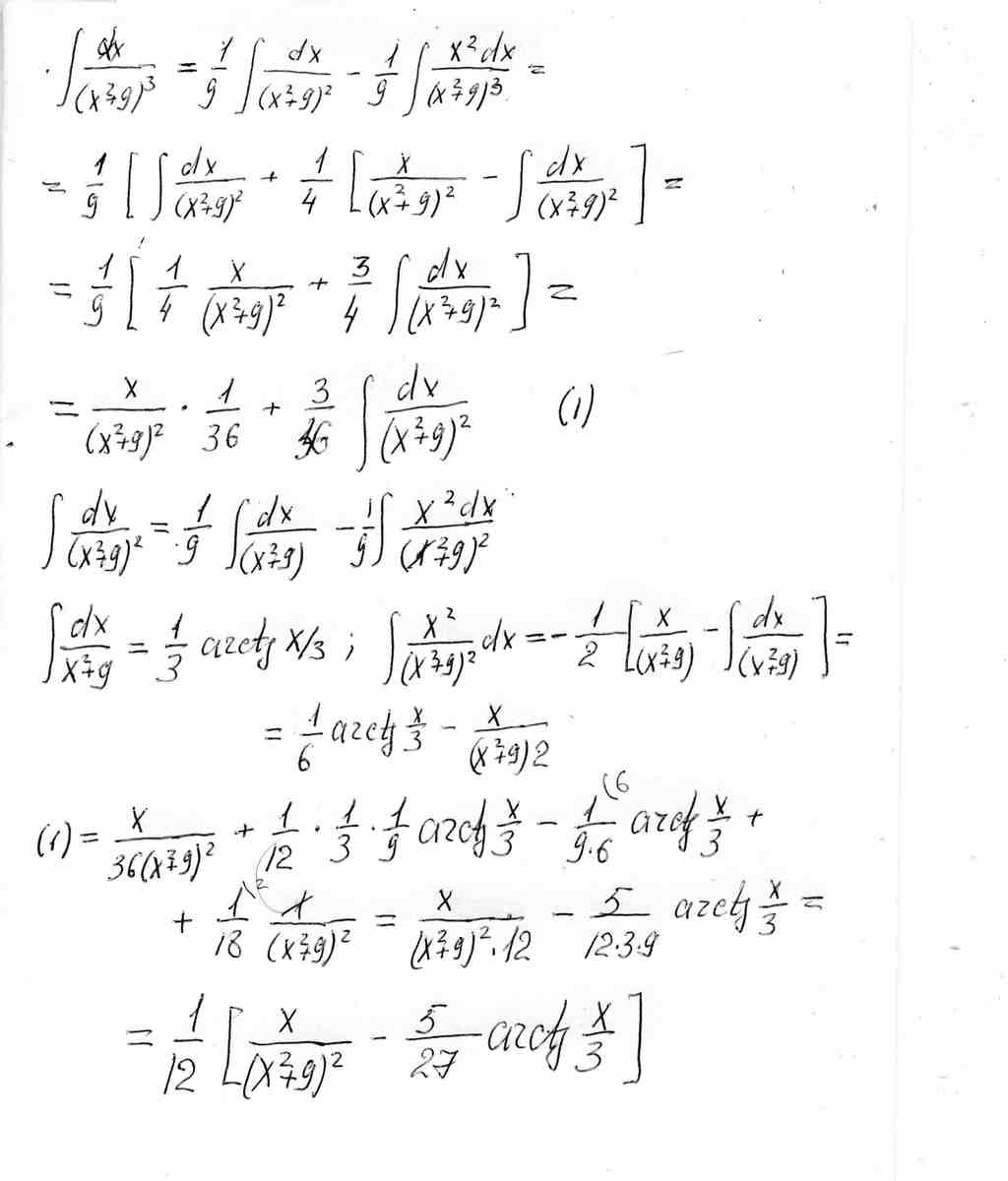
Автор ответа:
0
Посчитаем интеграл общего вида
Отсюда
учититывая, что
Отсюда
Приложения:
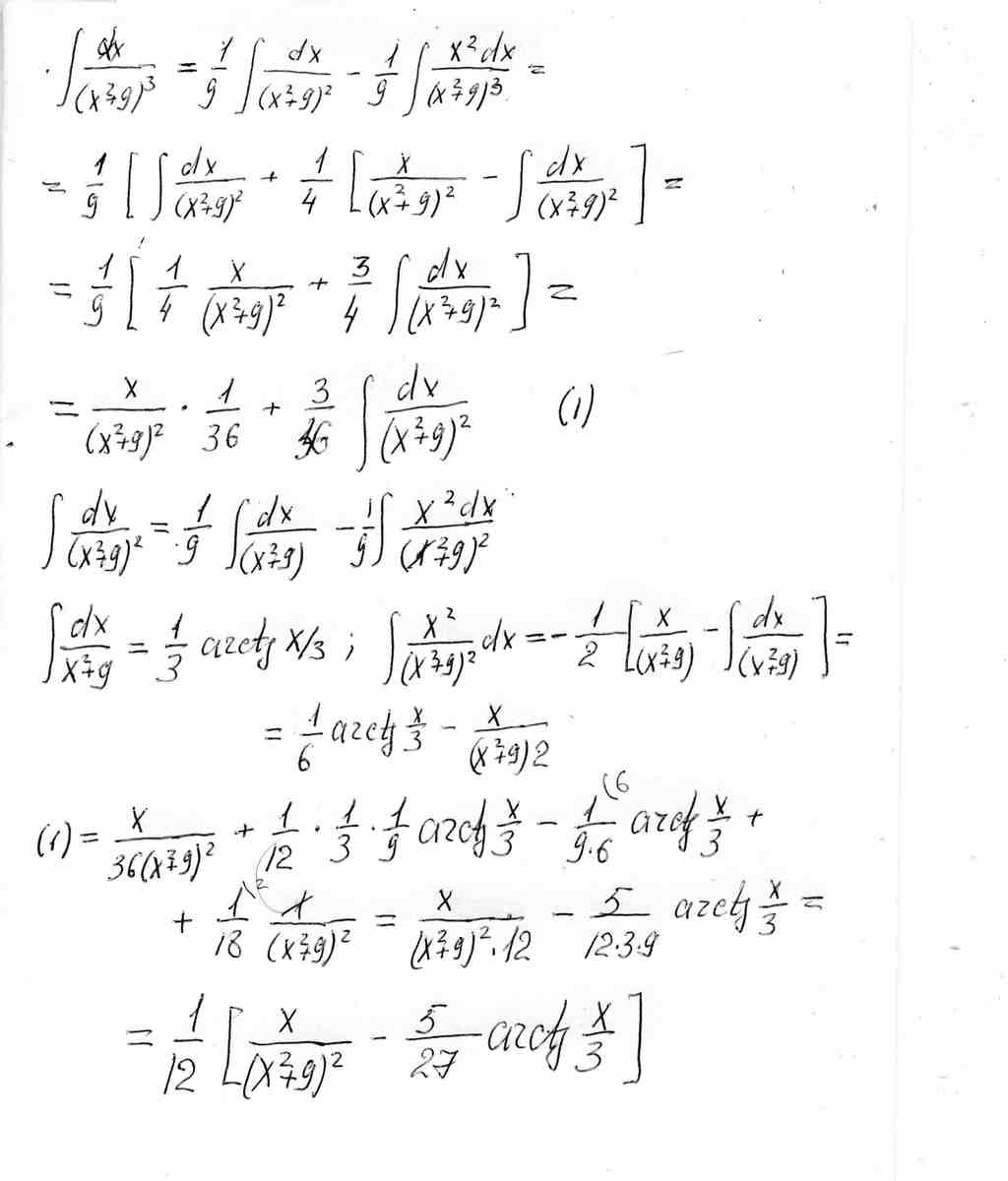
Похожие вопросы
Предмет: История,
автор: runner110
Предмет: Русский язык,
автор: egormal650
Предмет: Оʻzbek tili,
автор: tfier
Предмет: Математика,
автор: Lizunya2001
Предмет: Математика,
автор: Полино4каlove