Question

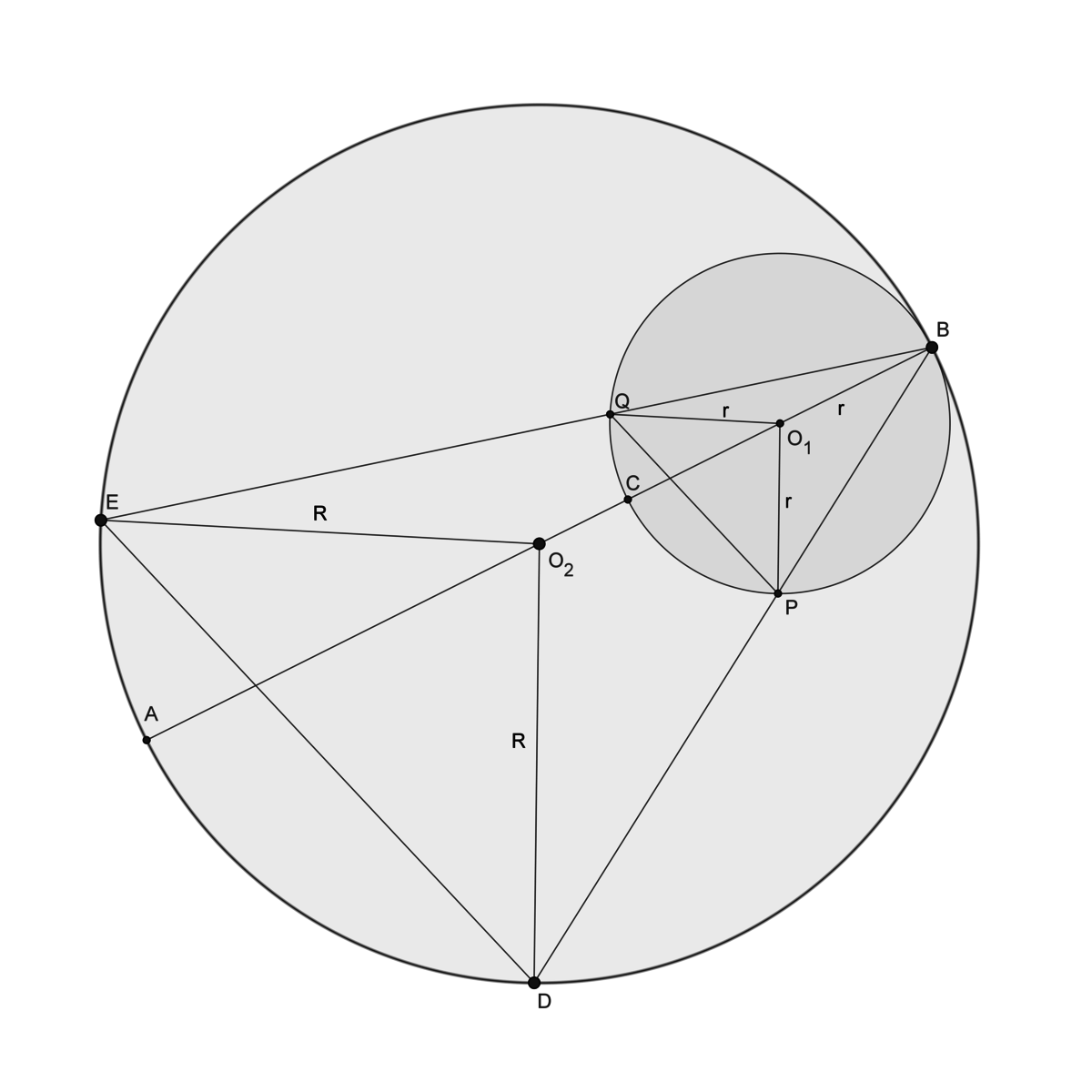
На диаметре аб отмечена точка С. Хорды BD и BE пересекают окружность с диаметром BC в точках P и Q соотвественно. Докажите что угол BED равен углу BQP и угол BDE равен углу BPQ

Answer 1

Если обозначить радиус большой окружности R, радиус маленькой r, то BP=2r·cos∠ABD, BD=2R·cos∠ABD. Значит BP/BD=r/R. Аналогично, BQ=2r·cos∠ABE, BE=2R·cos∠ABE. Значит BQ/BE=r/R, т.е. BP/BD=BQ/BE. Т.е.треугольники PBQ и DBE подобны по углу и двум прилажащим пропорциональным сторонам. Значит их соответствующие углы равны, т.е. ∠BED=∠BQP и ∠BDE=∠BPQ.