Угол между диаметром АВ и хордой АС равен 30*. Через точку С проведена касательная, пересекающая прямую АВ в точке Е.Найдите СЕ, если радиус окружности 6см. Решение.
Ответы
АВ - диам.=:L BCA = 90⁰ и ΔАВС - прям.,
тогда АВ = 12 см, ВС = ½ АВ = 6 см.
L СВЕ =180⁰ - LСВА = 180⁰ - 60⁰ = 120⁰ (они смеж.).
L BCE = 30⁰
В Δ ВСЕ: L E = 180⁰- (120⁰+30⁰) = 30⁰, т.е. ΔВСЕ - равнобедренный ( ВЕ = ВС=6).
По теореме косинусов:
СЕ =√( ВЕ²+ВС²-2·ВЕ·ВС·сos B) = √(6²+6² -2· 6·6·cos 120⁰) = √(72-36·2·(-0,5))=
=√36·3 = 6√3
Ответ: 6√3 cм .
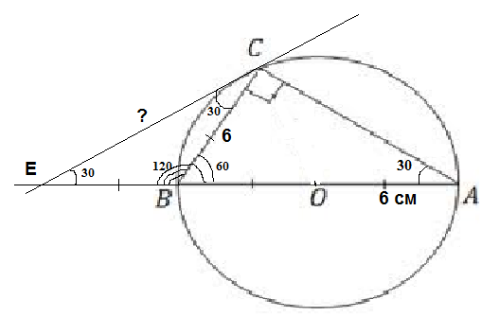
Дуга ВС = 2 х угол ВАС = 30 х 2 =60, Дуга АС = 180 - 60 =120
Угол СЕВ = 1/2 ( дуга АС - дуга ВС )= 1/2 (120-60)=30
Треугольник АСЕ равнобедренный, Угол СЕВ=углуСАВ =30, АС=СЕ,
В треугольнике АОС АО=ОС= радиусу =6, проводим высоту ОК, которая равна 1/2 АО, т.к. лежит против угла 30 в прямоугольном треугольнике ОК=6/2=3
АК = корень (АО в квадрате -ОК в квадрате)=корень (36-9) = 3 х корень3
АС= СЕ=2 х 3 х корень3=6 корень3
