Предмет: Геометрия,
автор: Шист
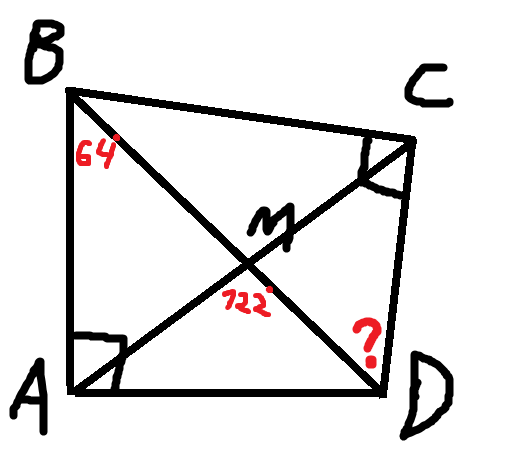
В четырехугольнике ABCD диагонали пересекаются в точке M,<BAD=<BCD=90, <AMD=122, <ABD=64. Найдите <BDC
Приложения:
Ответы
Автор ответа:
0
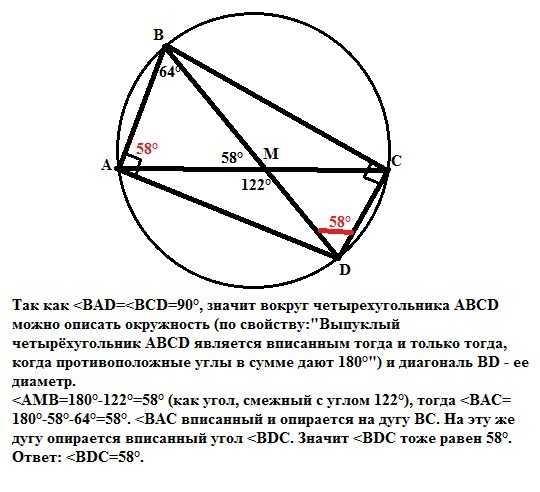
Так как <BAD=<BCD=90°, значит вокруг четырехугольника АВСD можно описать окружность (по свойству:"Выпуклый четырёхугольник ABCD является вписанным тогда и только тогда, когда противоположные углы в сумме дают 180°") и диагональ ВD - ее диаметр.
<AMB=180°-122°=58° (как угол, смежный с углом 122°), тогда <BAC=180°-58°-64°=58°. <BAC вписанный и опирается на дугу ВС. На эту же дугу опирается вписанный угол <BDC. Значит <BDC тоже равен 58°.
Ответ: <BDC=58°.
<AMB=180°-122°=58° (как угол, смежный с углом 122°), тогда <BAC=180°-58°-64°=58°. <BAC вписанный и опирается на дугу ВС. На эту же дугу опирается вписанный угол <BDC. Значит <BDC тоже равен 58°.
Ответ: <BDC=58°.
Приложения:
Автор ответа:
0
о госопди какой я дибииил, ааааа спасибооо!!!
Автор ответа:
0
Ну, зачем же так...
Похожие вопросы
Предмет: Литература,
автор: Аноним
Предмет: Математика,
автор: aidanabalma1990
Предмет: Қазақ тiлi,
автор: Аноним
Предмет: Математика,
автор: danshin77
Предмет: Информатика,
автор: Солнышко20010831