Предмет: Геометрия,
автор: cfahjyjdf
в треугольнике один из углов равен 40.найдите угол между биссектрисами двух других углов
Ответы
Автор ответа:
0
Пусть АВС - данный треугольник, угол А =40 градусов
ВК и CР - биссектриссы углов В и С соответственно, пересекаются в точке Т
тогда по определению биссектриссы
угол АВТ=угол СВТ=0.5*угол В
угол АСТ=ВСТ=0.5*угол С
Сумма углов треугольника равна 180 градусов
остюда
угол В+угол С=180 градусов - угол А=180 градусов -40 градусов=140 градусов
Искомый угол равен
угол ВСТ=180 градусов-0.5*угол В-0.5*угол С=180 градусов-0.5*(угол В+угол С)=180 градусов-0.5*140 градусов=180 градусов-70 градусов=110 градусов
Приложения:
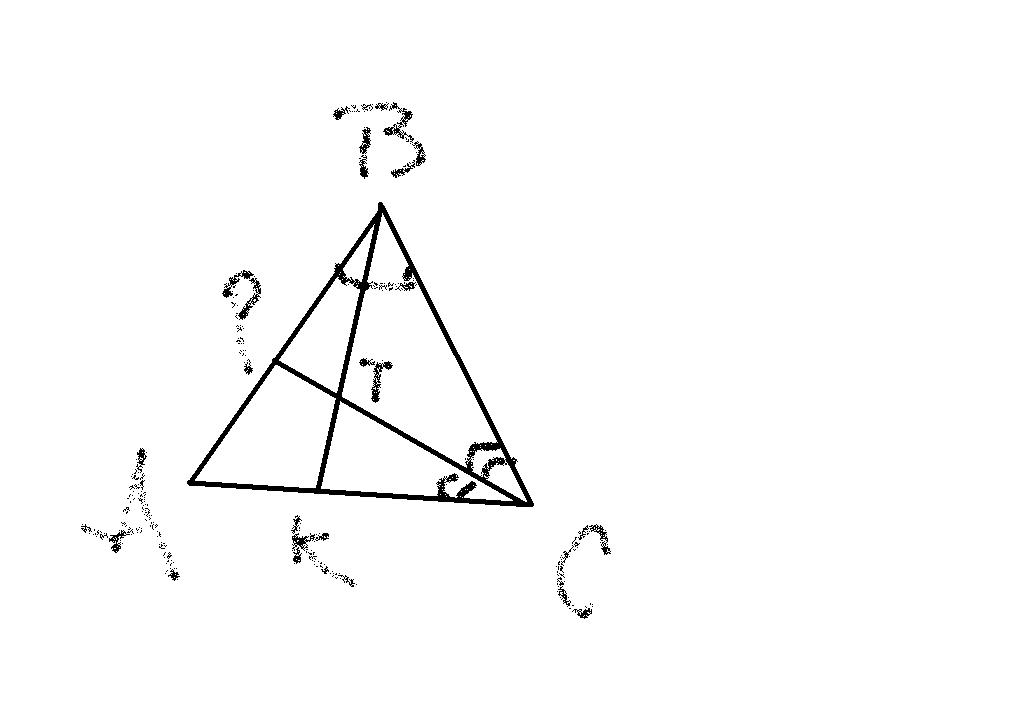
Похожие вопросы
Предмет: Английский язык,
автор: Аноним
Предмет: Алгебра,
автор: ilu71d
Предмет: Математика,
автор: palshis1808
Предмет: Алгебра,
автор: aleks000