Question

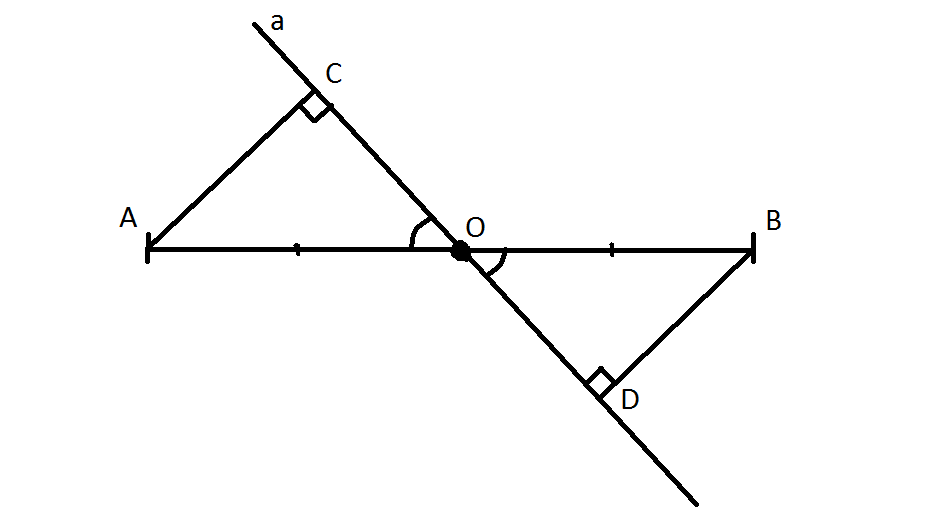
Через середину отрезка АВ проведена прямая а . Из точек А и В к прямой а проведены перпендикуляры АС и ВD. Докажите что АС=ВD.
Желательно с рисунком и подробно, спасибо!

Answer 1

Пусть O - середина отрезка AB, тогда перпендикуляры AC и BD, проведенные к прямой a, образуют два прямоугольных треугольника.

Угол AOC и угол BOD равны как вертикальные, следовательно треугольники AOC и BOD равные по гипотенузе и прилежащему к ней острому углу, следовательно AC = BD.

Answer 2

рисунок сделал как мог