Предмет: Геометрия, автор: Mintaka

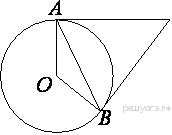
Касательные в точках A и B к окружности с центром O пересекаются под углом 24°. Найдите угол ABO. Ответ дайте в градусах.

Приложения:

Ответы

Автор ответа: ulasovage

0

Обозначим точку пересечения касательных буквой С .
По свойству касательных, проведённых к окружности из одной точки :
АС=ВС.
Рассмотрим Δ АВС - равнобедренный ⇒ ∠ САВ=∠СВА =(180°-24°)/2=78°
ОА ⊥ АС Значит ∠ САО= 90°
Аналогично ∠ СВО= 90°.
∠АВО= ∠СВО - ∠СВА=90° - 78°= 12°
ОТВЕТ :12°

Предыдущий вопрос

Следующий вопрос

Похожие вопросы

Предмет: История, автор: Bzudb1

привидите соответствие явление с событием до 40х годов СРОЧНО

6 лет назад

Предмет: Українська мова, автор: zaharserobobo

СРОЧНО 25Б
Вкажіть рядок у якому всі прикметники якісні
1)Залізні нерви, кам'яний будинок,вовча зграя
2)братів зошит, свіжий вітер,скляний посуд
3)ніжна квітка, кам'яне обличчя, світле волосся

6 лет назад

Предмет: Английский язык, автор: ES20011301

Написать по этому тексту 8 вопросов , ПОМОГИТЕ!!!
FOR THE LAST GENERATION Silicon Valley and Tokyo have been working to design computers that are ever easier to use. There is one thing, however, that has prevented the machines from becoming their user-friendliest: you still have to input data with a keyboard, and that can require you to do a lot of typing and to memorize a lot of elaborate commands.

Enter the clipboard computer. a technology that has been in-development for the last 20 years
but took hold in the mass market only this year. Clipboard PCs-which. as their name suggests, are not much bigger than an actual clipboard - replace the keyboard with a liquid crystal display (LCD)screen and an electronic stylus._Users input data by printing individual letters directly on the screen.

There are two technologies at work in a clipboard PC: one allows raw data to get into the computer and the other allows the computer to figure out what that data means.The first technology relies principelly on hardware and varies depending on the particular computer. In one system, marketed under the name GRIDPad.the computer's LCD screen is covered by a sheet ofBlass with a transparent conductive coating. Voltage is sent across the glass in horizontal and vertical lines forming a fine grid;at any point on the grid, the voltage is slightly different.When the stylus - which is essentially a voltmeter - touches the screen. it informs the computer of the voltage at that point. The computer uses this information to determine where the stylus is and causes a liquid crystal pixel to appear at those coordinates. The position of the stylas is monitored several hundred times a second, so as the stytus moves across the glass,whole strings of pixels are activated.'What we do is sort of connect the dots,' says Jeff Hawkins, the creator of GRIDPad. 'Users can then write whatever they want
on the screen with a kind of electronic ink.'

Making that writing comprehensible to the computer,however, requires the help of some powerful software. When the stylus is being used, the computer is programmed to look for moments when the tip does not touch the screen for a third of a second or more. Every time this happens - and it happens a lot when somebody is printing -the software assumes that one letter or number has been written. The pixel positions of 'What we do is sort of connect the dots,' says Jeff Hawkins, the creator of GRIDPad. 'Users can then write whatever they want on the screen with a kind of electronic ink.'

Making that writing comprehensible to the computer,however, requires the help of some powerful software. When the stylus is being used, the computer is programmed to look for moments when the tip does not touch the screen for a third of a second or more. Every time this happens - and it happens a lot when somebody is printing -the software assumes that one letter or number has been written. The pixel positions of this fresh character are then passed on to the computer's pottern recognition software, which instantly identifies the letter or number written.The software does this by first cleaning up the character -smoothing out crooked lines and removing errant dots. The remaining lines and curves are then compared with a series of templates in the computerts memory that represent hundreds of thousands of different versions of every letter in the English alphabet and all ten numerals. When the computer finds the closest match, it encodes the character in memory and displays it on the screen as if it had been typed.The entire process talces just a fraction of a second. To delete a word you simply draw a line through it. To move to the next page, you aick the stylus at the bottom of the screen as if you are flicking the page of a book.

There are a handful of clipboard computers now on the market,including CRIDPad, which is sold in the US; Penvision, manufactured by NCR and sold around the world:and Sony's Palmtop and Canon's Al Note,both sold only in Japan.IBM and Apple are also pouring millinons of dollars into the technology.

In addition to this hardware, a variety of software is also making its why to the market.
Depending on the power of the computer and the sophisttication of the software, clipboard
systems can be programmed to understand the particular quirks of a particular use's printing;
this is an especially useful feature in Japan, where elaborate kanji characters make up most of the wTitten language.Improvements in soft.ware may soon allow machines sold in the US to understand not only printing but continnous script as well.

Given such nexibility, the designers of clipboard computers are predicting big things - and a
big market -. for their products 'There's no doubt about it's says an optimistic Hawkins. 'You're going to own one of these things in the not-too-distant future.'

6 лет назад

Предмет: Математика, автор: alexmarser99

Ребят помогите сколько бедет 1милион прибавить 345536 и плюс 400500 скажите пррошу вас

9 лет назад

Предмет: Алгебра, автор: Markus755

Постройте график функции, заданной формулой:
f(x)=1,5-3x

9 лет назад