Question

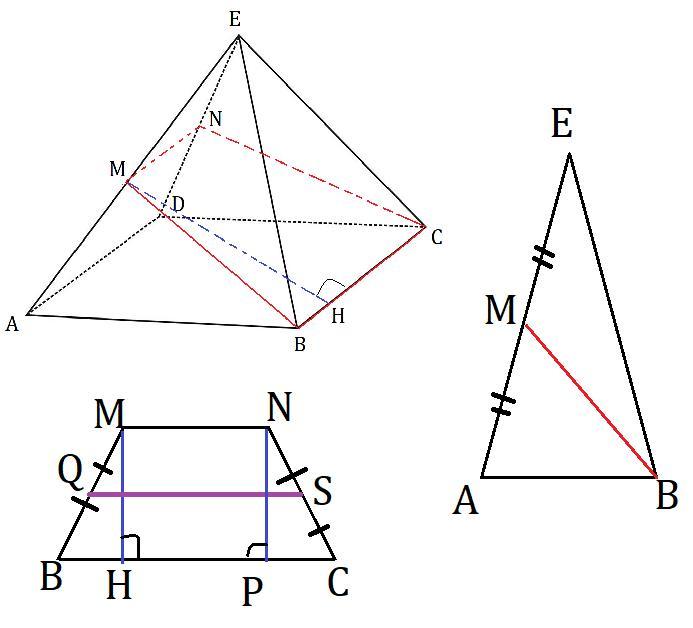
в правильной четырехугольной пирамиде со стороной основания а и боковым ребром b через сторону основания и среднюю линию противоположной боковой грани проведена плоскость вычислите плоскость сечения

Answer 1

Пирамида правильная и каждой стороне основания соответствует только одна боковая грань, поэтому всего возможно 4 сечения плоскостью в пирамиде с фиксированными точками, эти сечения все будут одинаковыми т.к. пирамида правильная и у ней есть ось симметрии, всё одинаково. Поэтому нужно найти только одну площадь сечения.

Так вот, пусть эта плоскость проходит через сторону основания BC и среднюю линию ΔAED - MN. Тогда сечение это равнобокая трапеция MNCB, т.к. MN║AD (как средняя линия ΔAED), AD║BC (как противоположные стороны квадрата ABCD) --> MN║BC;

И MB=NC как соответственные медина в равных треугольниках (ΔAEB и ΔDEC).

Площадь трапеции можно узнать через высоту трапеции и среднюю линию.

$MN=frac{1}{2} AD=frac{a}{2} \QS=frac{frac{a}{2}+a}{2} =frac{3a}{4}$ где QS это средняя линяя трапеции MNCB.

Найдём MB: в ΔAEB: по теореме косинусов:

$EB^2=AE^2+AB^2-2AE*AB*cos{(EAB)}=>\=>cos{(EAB)}=frac{AE^2+AB^2-EB^2}{2AE*AB}=\=frac{b^2+a^2-b^2}{2ab} =frac{a}{2b}$

∠EAB=∠MAB как углы с общими сторонами.

в ΔMBA: по теореме косинусов:

$MB^2=AM^2+AB^2-2AM*AB*cos{(MAB)}=\MB^2=(frac{b}{2})^2+a^2-2*frac{b}{2}*a*frac{a}{2b}=\=frac{b^2}{4}+a^2-frac{a^2}{2} =frac{b^2+2a^2}{4}$

В трапеции MNCB: проведём высоты MH и NP из вершин M и N на сторону BC соответственно. ΔMHB=ΔNPC по углу и гипотенузе. Значит BH=PC

В ΔMHB: по теореме пифагора:

$MH^2=MB^2-BH^2=frac{b^2+2a^2}{4}-(frac{a-frac{a}{2}}{2})^2=\frac{4b^2+4*2a^2-a^2}{16} =frac{4b^2+7a^2}{16}$

Зная высоту и среднюю линию находим площадь:

$S=QS*MH=frac{3a}{4}*sqrt{frac{4b^2+7a^2}{16}}=\=frac{3a}{16}*sqrt{4b^2+7a^2}$

Ответ: (3a/16)*√(7a²+4b²).