Предмет: Геометрия,
автор: okvmr232
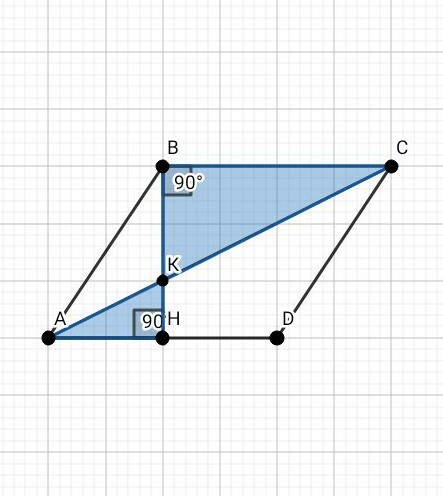
ABCD - ромб, BH - его высота. AB = 15, AH = 12 найти длины отрезков BK и KН . Точка К-пересечение прямых ВН и АС, точка Н лежит на стороне АD.
Ответы
Автор ответа:
0
В ромбе все стороны равны →
АВ = ВС = CD = AD = 15
HD = AD – AH = 15 - 12 = 3
Рассмотрим ∆ ВАН (угол АНВ = 90°):
По теореме Пифагора:
АВ² = АН² + ВН²
ВН² = 15² - 12²
ВН = 225 - 144 = 81
ВН = 9
∆ АКН подобен ∆ ВКС по двум углам
угол ВСА = угол CAD – как накрест лежащие углы при параллельных прямых ВС и AD и секущей АС
угол АНВ = угол СВН = 90° – ВН - высота ромба
Составим отношения сходственных сторон:
ВС/ АН= ВК/ КН = КС/ АК →
ВК / КН = 15 / 12 = 5 / 4
Но ВН = 9
Значит, ВК = 5 , КН = 4
ОТВЕТ: ВК = 5 , КН = 4
АВ = ВС = CD = AD = 15
HD = AD – AH = 15 - 12 = 3
Рассмотрим ∆ ВАН (угол АНВ = 90°):
По теореме Пифагора:
АВ² = АН² + ВН²
ВН² = 15² - 12²
ВН = 225 - 144 = 81
ВН = 9
∆ АКН подобен ∆ ВКС по двум углам
угол ВСА = угол CAD – как накрест лежащие углы при параллельных прямых ВС и AD и секущей АС
угол АНВ = угол СВН = 90° – ВН - высота ромба
Составим отношения сходственных сторон:
ВС/ АН= ВК/ КН = КС/ АК →
ВК / КН = 15 / 12 = 5 / 4
Но ВН = 9
Значит, ВК = 5 , КН = 4
ОТВЕТ: ВК = 5 , КН = 4
Приложения:
Похожие вопросы
Предмет: Литература,
автор: saskehard
Предмет: Қазақ тiлi,
автор: talsynhanskaa
Предмет: Математика,
автор: dfgjv
Предмет: Математика,
автор: пллплпл7951
Предмет: Алгебра,
автор: olgatchuprova2