Предмет: Геометрия,
автор: KristinaPimenova
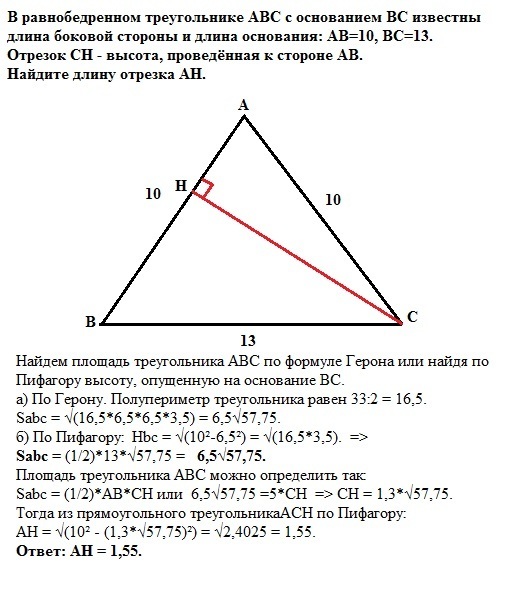
В равнобедренном треугольнике ABC c основанием BC известны длина боковой стороны и длина основания: AB=10, BC=13. Отрезок CH - высота, проведённая к
стороне AB. Найдите длину отрезка АН.
Ответы
Автор ответа:
0
Найдем площадь треугольника АВС по формуле Герона или найдя по Пифагору высоту, опущенную на основание ВС.
а) По Герону. Полупериметр треугольника равен 33:2 = 16,5.
Sabc = √(16,5*6,5*6,5*3,5) = 6,5√57,75.
б) По Пифагору: Hbc = √(10²-6,5²) = √(16,5*3,5). =>
Sabc = (1/2)*13*√57,75 = 6,5√57,75.
Площадь треугольника АВС можно определить так:
Sabc = (1/2)*AB*CH или 6,5√57,75 =5*СН => СН = 1,3*√57,75.
Тогда из прямоугольного треугольника АСН по Пифагору:
АН = √(10² - (1,3*√57,75)²) = √2,4025 = 1,55.
Ответ: АН = 1,55.
Приложения:
Автор ответа:
0
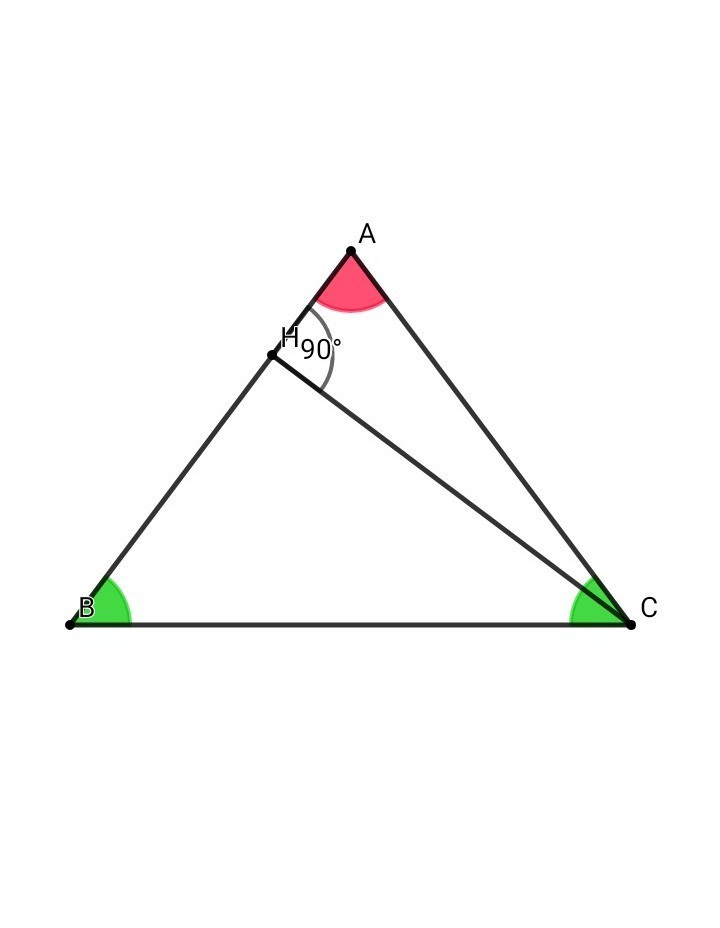
• Рассмотрим тр. АВС ( АВ = АС):
По теореме косинусов:
ВС^2 = АВ^2 + АС^2 - 2•АВ•АС•cosA
13^2 = 10^2 + 10^2 - 2•10•10•cosA
169 = 100 + 100 - 200•cosA
cosA = 31 / 200
• Рассмотрим тр. АНС (угол АНС = 90°):
cosA = AH / AC
31 / 200 = AH / 10
AH = 31 / 20 = 155 / 100 = 1,55
ОТВЕТ: 1,55
Приложения:
Похожие вопросы
Предмет: Қазақ тiлi,
автор: temir52
Предмет: История,
автор: mahamgalikyzym
Предмет: Українська мова,
автор: solomiiahryniuk2008
Предмет: Математика,
автор: vika1234562414